第三章 硬件描述语言VERILOG
本节的文档编号:001100000034
需要看对应的视频,请点击视频编号:001100000034
1、本节主要介绍硬件描述语言——Verilog HDL语言的演进过程以及其市场地位和诸多优点。
2、这是ALTERA和VIVADO文档
第1节 Verilog的历史
在传统硬件电路的设计方法中,当设计工程师需要设计一个新的硬件、数字电路或数字逻辑系统时,需要为此设计并画出一张线路图,随后在CAE(计算机辅助工程分析)工作站上进行设计。所设计的线路图由线和符号组成,其中线代表了线路,符号代表了基本设计单元,其取自于工程师构造此线路图使用的零件符号库。对于不同逻辑器件的设计,需要选择对应的符号库,如当设计工程师选择的时标准逻辑器件(74系列等)作为板级设计线路图,那么此线路图的符号则需要取自标准逻辑零件符号库;若设计工程师进行了ASIC设计,线路图的符号就要取自ASIC库专用的宏单元。
这就是传统的原理图设计方法,原理图设计法存在着许多弊端,如当设计者想要实现线路图的逻辑优化时,就需要利用EDA工具或者人工进行布尔函数逻辑优化。除此之外,传统原理图设计还存在难以验证的缺点,设计工程师想要验证设计,必须通过搭建硬件平台(比如电路板),为设计验证工作带来了麻烦。
随着人们对于科技的要求与期待越来越高,电子设计技术发展也越来越快,设计的集成度、复杂程度也逐渐加深,传统的设计方法已经无法满足高级设计的需求,最终出现了借助先进EDA工具的一种描述语言设计方法,可以对数字电路和数字逻辑系统进行形式化的描述,这种语言就是硬件描述语言。硬件描述语言,英文全称为Hardware Description Language,简称HDL,HDL是一种用形式化方法来描述数字电路和数字逻辑系统的语言。设计工程师可以使用这种语言来表述自己的设计思路,通过利用EDA工具进行仿真、自动综合到门级电路,最终在ASIC或FPGA实现其功能。
以2输入的与门为例来对比原理图设计方法与HDL设计方法之间的区别,在传统的设计方法中设计2输入与门可能需到标准器件库中调用74系列的器件,但在硬件描述语言中“&”就是一个与门的形式描述,“C = A & B”就是一个2输入与门的描述。而“&”就代表了一个与门器件。
硬件描述语言发展至今已有二十多年历史,当今业界的标准中(IEEE标准)主要有VHDL和 Verilog HDL 这两种硬件描述语言。本书采用的是VerilogHDL硬件描述语言,接下来着重对其发展的历史及特点进行介绍。
Verilog HDL 语言最初是在1983年由Gateway Design Automation公司为其模拟器产品开发的硬件建模语言,当时这只是公司产品的专用语言。随着公司模拟、仿真器产品的广泛使用,Verilog HDL 作为一种实用语言逐渐为众多设计者所接受。1990年一次致力于增加语言普及性的活动中,Verilog HDL 语言被推向公众领域从而被更多人熟知。
Open Verilog International(OVI)是促进 Verilog 发展的国际性组织。1992 年,OVI 决定致力于推广Verilog OVI 标准成为IEEE 标准。这一推广最后获得成功,Verilog 语言于1995 年成为IEEE 标准,称为IEEE Std1364-1995。其完整标准在Verilog 硬件描述语言参考手册中有详细描述。
Verilog HDL语言具有许多优点,例如Verilog HDL 语言提供了编程语言接口,通过该接口可以在模拟、验证期间从设计外部访问设计,包括模拟的具体控制和运行。 Verilog HDL 语言不仅定义了语法,而且对每个语法结构都定义了清晰的模拟、仿真语义。因此,用这种语言编写的模型能够使用Verilog 仿真器进行验证。Verilog HDL 提供了扩展的建模能力,其中许多扩展最初很难理解,但是Verilog HDL 语言的核心子集非常易于学习和使用,这对大多数建模应用来说已经足够。当然,完整的硬件描述语言足以对从最复杂的芯片到完整的电子系统进行描述。
第2节 综合和仿真
2.1 综合
Verilog是硬件描述语言,顾名思义,就是用代码的形式描述硬件的功能,最终在硬件电路上实现该功能。在Verilog描述出硬件功能后需要使用综合器对Verilog代码进行解释并将代码转化成实际的电路来表示,最终产生实际的电路,也被称为网表。这种将Verilog代码转成网表的工具就是综合器。

图1.3- SEQ 图1.3- * ARABIC1综合器的功能
上图左上角是一段Verilog代码,该代码实现了一个加法器的功能。在经过综合器解释后该代码被转化成一个加法器电路。QUARTUS、ISE和VIVADO等FPGA开发工具都是综合器,而在集成电路设计领域常用的综合器是DC。
2.2 仿真
在FPGA设计的过程中,不可避免会出现各种BUG。如果在编写好代码、综合成电路、烧写到FPGA后才发现问题,此时再去定位问题就会非常地困难。而在综合前,设计师可以在电脑里通过仿真软件对代码进行仿真测试,检测出BUG并将其解决,最后再将程序烧写进FPGA。一般情况下可以认为没有经过仿真验证的代码,一定是存在BUG的。
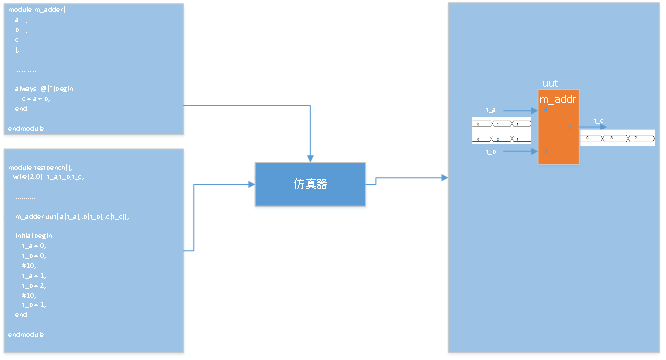
图1.3- SEQ 图1.3- * ARABIC2仿真器的功能
为了模拟真实的情况,需要编写测试文件。该文件也是用Verilog编写的,其描述了仿真对象的输入激励情况。该激励力求模仿最真实的情况,产生最接近的激励信号,将该信号的波形输入给仿真对象,查看仿真对象的输出是否与预期一致。需要注意的是:在仿真过程中没有将代码转成电路,仿真器只是对代码进行仿真验证。至于该代码是否可转成电路,仿真器并不关心。
由此可见,Verilog的代码不仅可以描述电路,还可以用于测试。事实上,Verilog定义的语法非常之多,但绝大部分都是为了仿真测试来使用的,只有少部分才是用于电路设计,详细可以参考本书的“可综合逻辑设计”一节。Verilog中用于设计的语法是学习的重点,掌握好设计的语法并熟练应用于各种复杂的项目是技能的核心。而其他测试用的语法,在需要时查找和参考就已经足够了。本书旨在方便本科、研究生的教学,因此将重点讲解设计用的语法。
2.3 可综合设计
Verilog硬件描述语言有类似高级语言的完整语法结构和系统,这些语法结构的应用给设计描述带来很多方便。但是,Verilog是描述硬件电路的,其建立在硬件电路的基础之上。而有些语法结构只是以仿真测试为目的,是不能与实际硬件电路对应起来的。也就是说在使用这些语法时,将一个语言描述的程序映射成实际硬件电路中的结构是不能实现的,也称为不可综合语法。
综合就是把编写的rtl代码转换成对应的实际电路。比如编写代码assign a=b&c;EDA综合工具就会去元件库里调用一个二输入与门,将输入端分别接上b和c,输出端接上a。
同样地,如果设计师编写了一些如下所示的语句
assign a=b&c;
assign c=e|f;
assign e=x^y;
……
综合工具就会像搭积木一样把这些“逻辑”电路用一些“门”电路来搭起来。当然,工具会对必要的地方做一些优化,比如编写一个电路assing a=b&~b,工具就会将a恒接为0,而不会去调用一个与门来搭这个电路。
综述所述,“综合”要做的事情有:编译rtl代码,从库里选择用到的门器件,把这些器件按照“逻辑”搭建成“门”电路。
不可综合,是指找不到对应的“门”器件来实现相应的代码。比如“#100”之类的延时功能,简单的门器件是无法实现延时100个单元的,还有打印语句等,也是门器件无法实现的。在设计的时候要确保所写的代码是可以综合的,这就依赖于设计者的能力,知道什么是可综合的代码,什么是不可综合的代码。对于初学者来说,最好是先记住规则,遵守规则,先按规则来设计电路并在这一过程中逐渐理解,这是最好的学习路径。
下面表格中列出了不可综合或者不推荐使用的代码。
表1.3- SEQ 表1.3- * ARABIC1不可综合或不推荐使用的代码
|
代码 |
要求 |
|
initial |
严禁在设计中使用,只能在测试文件中使用。 |
|
task/function |
不推荐在设计中使用,在测试文件中可用。 |
|
for |
在设计中、测试文件中均可以使用。但在设计中多数会将其用错,所以建议在初期设计时不使用,熟练后按规范使用 |
|
while/repeat/forever |
严禁在设计中使用,只能在测试文件中使用 |
|
integer |
不推荐在设计中使用 |
|
三态门 |
内部模块不能有三态接口,三态门只有顶层文件才使用。三态门目的是为了节省管脚,FPGA内部完全没有必要使用。关于三态门的介绍,请看后续三态门章节内容 |
|
casex/casez |
设计代码内部不能有X态和Z态,因此casez、casex设计时不使用。 |
|
force/wait/fork |
严禁在设计中使用,只能在测试文件中使用 |
|
#n |
严禁在设计中使用,只能在测试文件中使用 |
下表为推荐使用的设计代码。
表1.3- SEQ 表1.3- * ARABIC2推荐使用的代码及其说明
|
代码 |
备注 |
|
reg/wire |
设计中所有的信号类型定义,只有reg和wire两种 |
|
parameter |
设计代码中所有的位宽、长度、状态机命名等,建议都用参数表示,阅读方便并且修改容易。 |
|
assign/always |
程序块主要部分,至简设计法对always使用有严格规范。 组合逻辑格式为: always@(*) begin 代码语句; end 或者用assign
时序逻辑格式为: always@(posedge clk or negedgerst_n) begin if(rst_n==1’b0)begin 代码语句; end else begin 代码语句; end end 时序逻辑中,敏感列表一定是clk的上升沿和复位的下降沿、最开始必须判断复位。详细见本章组合逻辑和时序逻辑一节。 |
|
if else和case |
always里面的语句,使用if else和case两种方法用来作选择判断,可以完成全部设计。 |
|
算术运算符 (+,-,×,/,%) |
可以直接综合出相对应的电路。但除法和求余运算的电路面积一般比较大,不建议直接使用除法和求余。 |
|
赋值运算符(=,<=) |
时序逻辑用“<=”,组合逻辑用“=”;其他情况不存在。 |
|
关系运算符(==,!=,>,<,>=,<=,) |
详细见本章组合逻辑一节 |
|
逻辑运算符(&&,||,!) |
|
|
位运算符(~,|,^,&) |
|
|
移位运算符(<<,>>) |
|
|
拼接运算符({ }) |
第3节 模块结构
3.1 模块介绍
模块(module)是Verilog 的基本描述单位,是用于描述某个设计的功能或结构及与其他模块通信的外部端口。
模块在概念上可等同一个器件,就如调用通用器件(与门、三态门等)或通用宏单元(计数器、ALU、CPU)等。因此,一个模块可在另一个模块中调用,一个电路设计可由多个模块组合而成。一个模块的设计只是一个系统设计中的某个层次设计,模块设计可采用多种建模方式。
Verilog 的基本设计单元是“模块”。采用模块化的设计使系统看起来更有条理也便于仿真和测试,因此整个项目的设计思想就是模块套模块,自顶向下依次展开。在一个工程的设计里,每个模块实现特定的功能,模块间可进行层次的嵌套。对大型的数字电路进行设计时,可以将其分割成大小不一的小模块,每个小模块实现特定的功能,最后通过由顶层模块调用子模块的方式来实现整体功能,这就是Top-Down的设计思想。本书主要以Verilog硬件描述语言为主,模块是Verilog的基本描述单位,用于描述每个设计的功能和结构,以及其他模块通信的外部接口。
模块有五个主要部分:端口定义、参数定义(可选)、 I/O说明、内部信号声明、功能定义。模块总是以关键词module开始,以关键词endmodule结尾。它的一般语法结构如下所示:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
module module_name(
rst_n , //端口2,复位 dout //其他信号,如dout );
parameter DATA_W = 8;
input rst_n ; //输入信号定义output[DATA_W-1:0] dout; //输出信号定义
reg [DATA_W-1:0] dout; //信号类型
(reg、wire)定义
//……………以下为描述功能部分…………//
always@(*)begin end
//时序逻辑写法 always@(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin
else begin end end
endmodule |
下面详细分析一下这段代码:
3.2 模块名和端口定义
第1至5行声明了模块的名字和输入输出口。其格式如下:
module 模块名(端口 1,端口 2,端口 3,……);
其中模块是以module开始,以endmodule结束。模块名是模块唯一的标识符,一般建议模块名尽量用能够描述其功能的名字来命名,并且模块名和文件名相同。
模块的端口表示的是模块的输入和输出口名,也是其与其他模块联系端口的标识。
3.3 参数定义
第8行参数定义是将常量用符号代替以增加代码可读性和可修改性。这是一个可选择的语句,用不到的情况下可以省略,参数定义一般格式如下:
parameter DATA_W = x;
3.4 接口定义
第9至12行是I/O(输入/输出)说明,模块的端口可以是输入端口、输出端口或双向端口。其说明格式如下。
输入端口: input [信号位宽-1 : 0] 端口名 1;
input [信号位宽-1 : 0] 端口名 2;
……;
输出端口: output [信号位宽-1 : 0] 端口名 1;
output [信号位宽-1 : 0] 端口名 2;
……;
双向端口:inout [信号位宽-1 : 0] 端口名 1;
inout [信号位宽-1 : 0] 端口名 2;
……;
3.5 信号类型
第14至17行定义了信号的类型。这些信号是在模块内使用到的信号,并且与端口有关的 wire 和 reg 类型变量。其声明方式如下:
reg [width-1 : 0] R 变量 1, R 变量 2 ……;
wire [width-1 : 0] W 变量 1,W 变量 2……;
如果没有定义信号类型,默认是wire型,并且信号位宽为1。
3.6 功能描述
第21至31行是功能描述部分。模块中最重要的部分是逻辑功能定义部分,有三种方法可在模块中产生逻辑。
1. 用“assign”声明语句,如描述一个两输入与门:assign a = b & c。详细功能见“功能描述-组合逻辑”一节。
2. 用“always”块。即前面介绍的时序逻辑和组合逻辑。
3. 模块例化。详细功能见“模块例化”一节。
3.7 模块例化
对数字系统的设计一般采用的是自顶向下的设计方式,可将系统划分成几个功能模块,每个功能模块再划分成下一层的子模块。每个模块的设计对应一个module ,每个module 设计成一个Verilog HDL 程序文件。因此,对一个系统的顶层模块采用结构化设计,即顶层模块分别调用了各个功能模块。
一个模块能够在另外一个模块中被引用,这样就建立了描述的层次。模块实例化语句形式如下:
module_nameinstance_name(port_associations) ;
信号端口可以通过位置或名称关联,但是关联方式不能够混合使用。端口关联形式如下:
port_expr / /通过位置。
.PortName (port_expr) / /通过名称。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
module and (C,A,B); input A,B; output C; //省略 endmodule //在下面的“and_2”块中对上一模块“and”进行例化,可以有两种方式: module and_2(xxxxx) ... //方式一:实例化时采用位置关联,T3对应输出端口C,A对应A,B对应B。 and A1 (T3, A, B ); //方式二:实例化时采用名字关联,.C是and 器件的端口,其与信号T3相连 and A2( .C(T3), .A(A), .B(B)); … endmodule; |
建议:在例化的端口映射中请采用名字关联,这样,当被调用的模块管脚改变时不易出错。
在实例化中,可能有些管脚没用到,可在映射中采用空白处理,如:
|
1 2 3 4 5 6 |
DFF d1 ( .Q(QS), .Qbar ( ), // 该管脚悬空 .Data (D ) , .Preset ( ), // 该管脚悬空 .Clock (CK) ); //名称对应方式。 |
输入管脚悬空端口的输入为高阻 Z,由于输出管脚是被悬空的,该输出管脚废弃不用。
第4节 信号类型
Verilog HDL的信号类型有很多种,主要包括两种数据类型:线网类型(net type) 和寄存器类型(reg type)。在进行工程设计的过程中也只会使用到这两个类型的信号。
4.1 信号位宽
定义信号类型的同时,必须定义好信号的位宽。默认信号的位宽是1位,当信号的位宽为1时可不表述,如定义位宽为1的wire型信号a可直接用“wire a;”来表示。但信号的位宽大于1位时就一定要表示出来,如用“wire [7:0]”来表示该wire型信号的位宽为8位。
信号的位宽取决于要该信号要表示的最大值。该信号能表示的无符号数最大值是:2n-1,其中n
表示该信号的位宽。例如,信号a的最大值为1000,那么信号a的位宽必须大于或等于10位。
下面分享一个位宽计算技巧:打开电脑的“计算器”后选用程序员模式,在在10进制下
输入信号值,如1000,随后可以查看信号位宽。
4.2 线网类型wire
线网类型用于对结构化器件之间的物理连线的建模,如器件的管脚,芯片内部器件如与门的输出
等。由于线网类型代表的是物理连接线,因此其不存储逻辑值,必须由器件驱动。通常用assign 进行赋值,如 assign A = B ^ C。
wire 类型定义语法如下:
wire [msb: lsb] wire1, wire2, . . .,wireN;
Ø msb和lsb定义了范围,表示了位宽。例如[7:0]是8位位宽,也就是可以表示成8’b0至8’b1111_1111;
Ø msb和lsb必须为常数值;
Ø 如果没有定义范围,缺省值为1位;
Ø 没有定义信号数据类型时,缺省为wire 类型。
Ø 注意数组类型按照降序方式,如[7:0] ,不要写成[0:7]。
下面对上述情况进行举例说明:
wire [3:0] Sat; // Sat为4 位线型信号
wire Cnt; //1 位线型信号
wire [31:0] Kisp, Pisp, Lisp ;// Kisp, Pisp, Lisp 都是32位的线型信号。
4.3 寄存器类型reg
reg 是最常用的寄存器类型,寄存器类型通常用于对存储单元的描述,如D型触发器、ROM 等。寄存器类型信号的特点是在某种触发机制下分配了一个值,在下一触发机制到来之前保留原值。但必须注意的是:reg 类型的变量不一定是存储单元,如在always语句中进行描述的必须是用reg 类型的变量。
reg 类型定义语法如下:
reg [msb: lsb] reg1, reg2, . . . reg N;
Ø msb和lsb定义了范围,表示了位宽。例如[7:0]是8位位宽,也就是可以表示成8’b0至8’b1111_1111;
Ø msb和lsb必须为常数值;
Ø 如果没有定义范围,缺省值为1位;
Ø 没有定义信号数据类型时,缺省为wire 类型,不是reg型。
Ø 对数组类型按照降序方式,如[7:0] ;不要写成[0:7]。
例如:
reg [3:0] Sat; // Sat为4 位寄存器型信号。
reg Cnt; //1 位寄存器。
reg [31:0] Kisp, Pisp, Lisp ; // Kisp, Pisp, Lisp 都是32位的寄存器型信号。
4.4 wire和reg的区别
reg型信号并不一定生成寄存器。针对什么时候使用wire类型,什么时候用reg类型这一问题,本书总结出一套解决方法:在本模块中使用always设计的信号都定义为reg型,其他信号都定义为wire型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
always @(posedge clk or negedge rst_n) begin if (rst_n==0) begin cnt1 <= 0; end else if(add_cnt1) begin if(end_cnt1) cnt1 <= 0; else cnt1 <= cnt1+1 ; end end assign add_cnt1 = end_cnt0; assign end_cnt1 = add_cnt1 && cnt1 == 8-1 ; |
上述代码中,cnt1是用always设计的,所以定义为reg型。add_cnt1和end_cnt不是由always产生的,所以定义为wire型。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
always @(*)begin if(cnt2==0) x = 475_000; else if(cnt2==1) x = 425_000; else if(cnt2==2) x = 350_000; else if(cnt2==3) x = 250_000; else if(cnt2==4) x = 100_000; else if(cnt2==5) x = 100_000; else if(cnt2==6) x = 250_000; else if(cnt2==7) x = 350_000; else if(cnt2==8) x = 425_000; else x = 475_000; end |
上述代码中,信号x是用always设计的,所以要定义为reg型。注意:实际的电路中信号x不是寄存器类型,但仍然定义为reg型。
|
1 2 3 4 5 6 7 |
QamCarrierQAM_Sync_inst( .clk ( clk_8 ), .rst_n ( rst_n ), .din ( data_buff ), .di ( Sync_Thre_real_i ), .dq ( Sync_Thre_imag_q ), .df ( df )); |
以上是例化的代码,其中df是例化模块的输出。由于df不是由always产生的,而是例化产生的,因此要定义成wire型。
第5节 功能描述-组合逻辑
5.1 程序语句
5.1.1 assign语句
assign语句是连续赋值语句,一般是将一个变量的值不间断地赋值给另一变量,两个变量之间就类似于被导线连在了一起,习惯上当做连线用。assign语句的基本格式是:
assign a = b (逻辑运算符)c …;
assign语句的功能属于组合逻辑的范畴,应用范围可以概括为一下几点:
(1)持续赋值;
(2)连线;
(3)对wire型变量赋值,wire是线网,相当于实际的连接线,如果要用assign直接连接,就用wire型变量,wire型变量的值随时发生变化。
需要说明的是,多条assign连续赋值语句之间互相独立、并行执行。
5.1.2 always语句
always 语句是条件循环语句,执行机制是通过对一个称为敏感变量表的事件驱动来实现的,下面会具体讲到。always 语句的基本格式是:
always @(敏感事件)begin
程序语句
end
always是“一直、总是”的意思,@后面跟着事件。整个always的意思是:当敏感事件的条件满足时,就执行一次“程序语句”。敏感事件每满足一次,就执行“程序语句”一次。
|
1 2 3 4 5 6 |
always @(a or b or d)begin if(sel==0) c = a + b; else c = a + d; end |
这段程序的意思是:当信号a或者信号b或者信号d发生变化时,就执行一次下面语句。在执行该段语句时,首先判断信号sel是否为0,如果为0,则执行第3行代码。如果sel不为0,则执行第5行代码。需要强调的是,a、b、c任意一个发生变化一次,2行至5行也只执行一次,不会执行第二次。
此处需要注意,仅仅sel这个信号发生变化是不会执行第2行到5行代码的,通常这并不符合设计者的想法。例如,一般设计者的想法是:当sel为0时c的结果是a+b;当sel不为0时c的结果是a+d。但如果触发条件没有发生改变,虽然sel由0变1,但此时c的结果仍是a+b。因此,这并不是一个规范的设计思维。
因此,按照设计者的想法重新对代码进行设计:当信号a或者信号b或者信号d或者信号sel发生变化时,就执行2行至5行。这样就可以确保sel信号值为0时,c的结果一定为a+b,当sel不为0时,c的结果一定是a+d。因此要在敏感列表中加入sel,其代码如下所示。
|
1 2 3 4 5 6 |
always @(a or b or d or sel)begin if(sel==0) c = a + b; else c = a + d; end |
当敏感信号非常多时很容易就会把敏感信号遗漏,为避免这种情况可以用“*”来代替。这个“*”是指“程序语句”中所有的条件信号,即a、b、d、sel(不包括c),也推荐这种写法,其具体代码如下所示。
|
1 2 3 4 5 6 |
always @(*)begin if(sel==0) c = a + b; else c = a + d; end |
这种条件信号变化结果立即变化的always语句被称为“组合逻辑”。
|
1 2 3 4 5 6 |
always @(posedge clk)begin if(sel==0) c <= a + b; else c <= a + d; end |
上述代码敏感列表是“posedge clk”,其中posedge表示上升沿。也就是说,当clk由0变成1的瞬间执行一次程序代码,即第2至5行,其他时刻c的值保持不变。要特别强调的是:如果clk没有由0变成1,那么即使a、b、d、sel发生变化,c的值也是不变的。
|
1 2 3 4 5 6 |
always @(negedge clk)begin if(sel==0) c <= a + b; else c <= a + d; end |
可以看到上述代码的敏感列表是“negedge clk”,其中negedg表示下降沿。也就是说,当clk由1变成0的瞬间执行一次程序代码,即第2至5行,其他时刻c的值保持不变。要特别强调的是,如果clk没有由1变成0,那么即使a、b、d、sel发生变化,c的值也是不变的。
|
1 2 3 4 5 6 7 8 9 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin c <= 0; end else if(sel==0) c <= a + b; else c <= a + d; end |
上述代码的敏感列表是“posedge clk or negedge rst_n”,也就是说,当clk由0变成1的瞬间,或者rst_n由1变化0的瞬间,执行一次程序代码,即第2至8行,其他时刻c的值保持不变。
这种信号边沿触发,即信号上升沿或者下降沿才变化的always,被称为“时序逻辑”,此时信号clk是时钟。注意:识别信号是不是时钟不是看名称,而是看这个信号放在哪里,只有放在敏感列表并且是边沿触发的才是时钟。而信号rst_n是复位信号,同样也不是看名字来判断,而是放在敏感列表中且同样边沿触发,更关键的是“程序语句”首先判断了rst_n的值,这表示rst_n优先级最高,一般都是用于复位。
设计时需要注意以下几点:
1、组合逻辑的always 语句中敏感变量必须写全,或者用“*”代替。
2、组合逻辑器件的赋值采用阻塞赋值“=,时序逻辑器件的赋值语句采用非阻塞赋值“<=”,具体原因见“阻塞赋值和非阻塞赋值”一节内容。
5.2 数字进制
5.2.1 数字表示方式
在Verilog中的数字表示方式,最常用的格式是:<位宽>’<基数><数值>,如4’b1011。
位宽:描述常量所含位数的十进制整数,是可选项。例如4’b1011中的4就是位宽,通俗理解就是4根线。如果没有这一项可以通过常量的值进行推断。例如’b1011可知位宽是4,而’b10010可推断出位宽为5。
基数:表示数值是多少进制。可以是b,B,d,D,o,O,h或者H,分别表示二进制、十进制、八进制和十六进制。如果没有此项,则缺省默认为十进制数。例如,二进制的4’b1011可以写成十进制的4’d11,也可以写成十六进制的4’hb或者八进制的4’o13,还可以不写基数直接写成11。综上所述,只要二进数相同,无论写成十进制、八进制和十六进制都是同样的数字。
数值:是由基数所决定的表示常量真实值的一串ASCII码。如果基数定义为 b或B,数值可以是0,1,x,X,z或Z。如果基数定义为 o或O,数值可以是2,3,4,5,6,7。如果基数定义为 h或H,数值可以是8,9,a,b,c,d,e,f,A,B,C,D,E,F。对于基数为d或者D的情况,数值符可以是任意的十进制数:0到9,但不可以是x或z。例如,4’b12是错误的,因为b表示二进制,数值只能是0、1、x或者z,不包含2。32’h12等同于32’h00000012,即数值未写完整时,高位补0。
5.2.2 二进制是基础
在数字电路中如果芯片A给芯片B传递数据,例如传递0或者1信息,可以将芯片A和芯片B通过一个管脚进行相连,然后由芯片A控制该管脚输出为高电平或者低电平,通过高低电平来表示0和1。芯片B检测到该管脚为低电平时,表示收到0,芯片B检测到该管脚为高电平时,表示收到1。

图1.3- SEQ 图1.3- * ARABIC3低电平表示0
反之,如果用低电平表示收到1,用高电平表示收到0可不可以呢?当然可以,只要芯片A和芯片B事先协定,芯片A要发数字1时会将该管脚置为低电平。芯片B检测到该管脚为低电平,表示收到了数字1,通信完成。

图1.3- SEQ 图1.3- * ARABIC4低电平表示1
一个管脚拥有高低电平两种状态,可以分别表示数字0和1的两种情况。如果芯片A要发数字0、1、2、3给芯片B又要如何操作呢?
可以让芯片A和芯片B连接两根管脚,即两条线:a和b。当两条线都为低电平时,表示发送数字0;当a为高电平b为低电平时,表示发送数字1;当a为低电平b为高电平时,表示发送数字2;当两条线都是高电平时,表示发送数字3。

图1.3- SEQ 图1.3- * ARABIC5两条线可以表示四种结果
按照同样的道理,芯片A要发送数据4,5,6,7给芯片B时,只要再添加一条线就可以了。三根线一共有8种状态,可以表示8个数字。综上所述,线的不同电平状态可以表示不同的含义,有多少种不同状态就可以表示多少个数字。
下面来思考一下如果芯片A要发送+1,-1,0,+2等数字给芯片B,这里的正负又该如何表示呢?参考前面的思路,线的高低电平表示的含义是由芯片双方向事先约定好的,既然如此则可以单用一根线来表示符号,例如低电平表示正数,高电平表示负数。
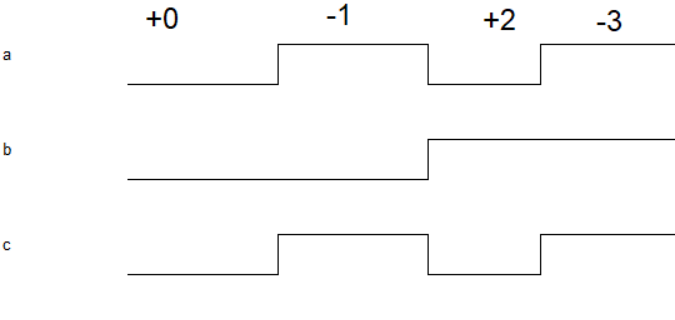
图1.3- SEQ 图1.3- * ARABIC6对正负数的表示方法
上图所示的三根线中用线c表示正负,其中0表示正数,1表示负数。用线a和线b表示数值,以3’b111为例,其可以解释为十进制数7,也可以解释为有符号数原码“-3”,也可以解释为有符号数补码“-1”,如何解释取决于工程师对二进制数的定义。只要该定义不影响到电路之间的通信就不会发生问题。因此数字中的“0”和“1”不仅可以表示字面上的数值含义,也可以表示其他意义,如正负符号等。同样的道理,在数字电路中二进制数是八进制、十进制、十六进制、有符号数、无符号数、小数等其他数制的根本。在FPGA设计中,不清楚小数、有符号数的计算方法的最根本原因是不清楚这些数据所对应的二进制值,只要理解了对应的二进制值,很多问题都可以解决。
下面通过例子让同学们更好的理解这一概念,很多初学者经常问,FPGA中如何实现小数计算呢?以“0.5+0.25”为例,众所周知0.5+0.25的结果为0.75,可以考虑0.5、0.25和0.75用二进制该如何表示?具体表示方法取决于工程师的做法,因为这种表示方法有很多种,例如定点小数,浮点小数,甚至如前面所讨论,用几根线自行来定义,只要能正常通信,那就没有问题。假设某工程师用三根线自行定义了二进制值所表示的小数值,如下表所示。
表1.3- SEQ 表1.3- * ARABIC3自定义二进制数值表
|
二进制值 |
定义 |
二进制值 |
定义 |
|
3’b000 |
0.1 |
3’b100 |
0.25 |
|
3’b001 |
0.5 |
3’b101 |
0.3 |
|
3’b010 |
0.75 |
3’b110 |
0.8 |
|
3’b011 |
0.2 |
3’b111 |
0 |
为了说明二进制值的意义是可以随便定义的,数字顺序为乱序。那为什么只有这几种小数呢?这是因为假定中的系统就只有这几种数字,如果想表示更多数字增加线的数量就可以了。
完成上面定义之后,要实现“0.5+0.25”就很容易了,其实就是3’b001和3’b100“相加”,期望得到3’b010。但是在该表中直接使用3’b001 + 3’b100,结果为“101”,这不是想要的结果,此时可以将代码写为:
|
1 2 |
If(a==3’b001 && b==3’b100) c<= 3’b010; |
当然,这只是其中一种写法,只要能实现所对应的功能且结果正确,任意写法都可以。
此处可能存在疑虑,0.1+0.8应该为0.9,但上面的表格中并没有0.9的表示。这其实是设计者定义的这个表格有缺陷,或者设计者认为不会出现这一情况。此处要表达的是:只要定义好对应的二进制数,很多功能都是很容易设计的。
当然,实际的工程中通常会遵守约定成俗的做法,没必要另辟蹊径。例如,下表是常用的定点小数的定义:
表1.3- SEQ 表1.3- * ARABIC4常用定点小数定义
|
二进制值 |
定义 |
二进制值 |
定义 |
|
3’b000 |
0.0 |
3’b100 |
0.5 |
|
3’b001 |
0.125 |
3’b101 |
0.625 |
|
3’b010 |
0.25 |
3’b110 |
0.75 |
|
3’b011 |
0.3725 |
3’b111 |
0.8725 |
此时如果要实现0+0.5=0.5,也就是3’b000和3’b100相加,期望能得到3’b100。可以发现直接用二进制3’b000+3’b100就能得到3’b100。
同样地,要实现0.125+0.75=0.8725,也就是3’b001和3’b110相加,期望能得到3’b111。可以发现直接用二进制3’b001+3’b110就能得到3’b111。
如果要实现0.5+0.75=1.25这一计算,可以看出此时1.25已经超出了表示范围,可以通过增加信号位宽或只表示小数位的做法解决这一问题。如果只是表示小数位则结果就是0.25,即3’b100和3’b110相加,期望得到3’b010。不难发现3’b100 + 3’b110 = 4’b1010,用3位表示就是3’b010,也就是0.25。综上所述可以看出,定点小数的计算并不复杂,定义好定点小数与二进制值之间的关系后直接进行计算即可。
5.2.3 不定态
前文中讲过数字电路只有高电平和低电平,分别表示1和0。但代码中经常能看到x和z,如1’bx,1’bz。那么这个x和z是什么电平呢?答案是并没有实际的电平来对应两者。x和z更多地是用来表示设计者的意图或者用于仿真目的,旨在告诉仿真器和综合器如何解释这段代码。
X态,称之为不定态,其常用于判断条件,从而告诉综合工具设计者不关心它的电平是多少,是0还是1都可以。
|
1 2 3 4 5 6 7 8 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin dout<= 0; end else if(din==4'b10x0)begin dout<= 1; end end |
上面的例子中可以看出判断条件是din==4’b10x0,该条件等价于din==4’b1000||din==4’b1010,其中“||”是“或”符号。
|
1 2 3 4 5 6 7 8 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin dout<= 0; end else if(din==4'b1000|| din==4'b1010)begin dout<= 1; end end |
然而在设计中直接写成din==4’b1000||din==4’b1010要好于写成“din==4’b10x0”,因为这样的写法更加直接和简单明了。
在仿真的过程中有些信号产生了不定态,那么设计者就要认真分析这个不定态是不是合理的。如果真的不关心它是0还是1,那么可以不解决。但建议所有信号都不应该处于不定态,写清楚其是0还是1,不要给设计添加“思考”的麻烦。
5.2.4 高阻态
Z态,一般称之为高阻态,表示设计者不驱动这个信号(既不给0也不给1),通常用于三态门接口当中。
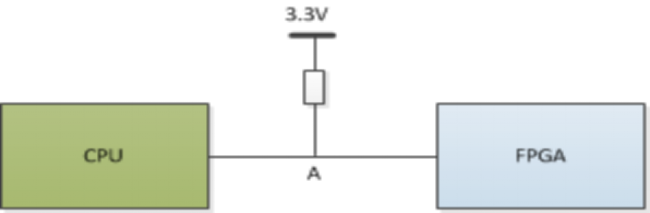
图1.3- SEQ 图1.3- * ARABIC7三态总线应用
上图就是三态总线的应用案例,图中的连接总线对于CPU和FPGA来说既为输入又为输出,是双向接口。一般的硬件电路中会将该线接上一个上拉电阻(弱上拉)或下拉电阻(弱下拉)。
当CPU和FPGA都不驱动该总线时,A点保持为高电平。当FPGA不驱动该总线,CPU驱动该总线时,A点的值就由CPU决定。当CPU不驱动该总线,FPGA驱动该总线时,A点的值就由FPGA决定。但FPGA和CPU不能同时驱动该总线,否则A的电平就不确定了,通常FPGA和CPU何时驱动总线是按事先协商的协议进行工作。
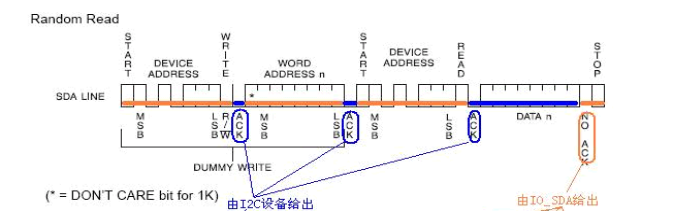
图1.3- SEQ 图1.3- * ARABIC8I2C总线协议
上图是典型的I2C的时序。I2C的总线SDA就是一个三态信号。I2C协议已规定好上面的时间中,哪段时间是由主设备驱动,哪段时间是由从设备驱动,双方都要遵守协议,不能存在同时驱动的情况。那么FPGA在设计中是如何做到“不驱动”这一行为呢?这是因为FPGA内部有三态门。
|
wr_en |
|
FPGA外部 |
|
FPGA内部 |
|
wr_data |
|
rd_data |
|
data |
图1.3- SEQ 图1.3- * ARABIC9FPGA内部三态门
三态门是一个硬件,上图是它的典型结构。三态门有四个接口,如上图所示的写使能wr_en、写数据wr_data、读数据rd_data以及与外面器件相连的三态信号data。
需要注意的是写使能信号,当该信号有效时三态门会将wr_data的值赋给三态线data,此时data的值由wr_data决定,当wr_data为0时data值为0;当wr_data为1时data值为1。而当写使能信号无效时,则不论wr_data值是多少都不会对外面的data值有影响,也就是不驱动。
在Verilog中以上功能是通过如下代码实现的:
|
1 2 |
assign data = (wr_en==1)?wr_data:1'bz; assign rd_data = data; |
当综合器看到这两行代码则知道要综合成三态门了,高阻z的作用正在于此。此外可以注意到硬件上用三态线是为了减少管脚,而在FPGA内部没有必要减少连线,所以使用三态信号是没有意义的。因此,建议各位在进行设计时不要在FPGA内部使用高阻态“z”,因为没有必要给自己添加“思考”的麻烦。当然,如果设计中使用了高阻态也不会报错,也可以实现功能。
总的来说高阻态“z”是表示“不驱动总线”这个行为,实际上数字电路就是高电平或者低电平,不存在其他电平的情况。
5.3 算术运算符
|
分类 |
功能 |
代码 |
电路示意图 |
备注 |
|
加法器 |
两数相加 |
always@(*) begin C =A+B; end |
|
本质上,运算逻辑都是由与门、或门等门逻辑搭建起来的电路,例如1位的加法就是S= A ^B;Cout= A&&B。 |
|
减法器 |
两数相减 |
always@(*) begin C =A-B; end |
|
|
|
乘法器 |
两数相乘 |
always@(*) begin C =A*B; end |
|
在二进制运算中,乘法运算实质上就是加法运算,例如1111*111 = (1111) + (11110) +(111100)。所以乘法器会比加法器消耗的资源多。 |
|
除法器 |
两数相除 |
always@(*) begin C =A/B; end |
|
二进制运算中,除法和求余涉及到加法、减法和移位等运算,所以除法和求余电路资源都非常大,在设计时要尽力避免除法和求余。如果一定要用到除法,尽量让除数为2的n次方,如2,4,8,16等。因为a/2实质就是a向右移1位;a/4实质就是a向右移2位。移位运算是不消耗资源的。 |
|
求余器 |
两数求余 |
always@(*) begin C =A%B; end |
|
算术运算符包括加法“+”、减法“-”、乘法“*”、除法“/”和求余“%”,其中常用的算术运算符主要有:加法“+”,减法“-”和乘法“*”。
注意,常用的运算中不包括除法和求余运算符,这是由于除法和求余不是简单的门逻辑搭建起来的,其所对应的硬件电路比较大。加减是最简单的运算,而乘法可以拆解成多个加法运算,因此加减法、乘法所对应的电路都比较小。而除法就不同了,同学们可以回想一下除法的步骤,其涉及到多次乘法、移位、加减法,所以除法对应的电路是复杂的,这也同时要求设计师在进行Verilog设计时要慎用除法。
5.3.1 加法运算符
首先学习加法运算符,在Verilog代码中可以直接使用符号“+”:
|
1 |
assign C=A + B; |
其电路示意图如下所示:

图1.3- SEQ 图1.3- * ARABIC10加法电路示意图
综合器可以识别加法运算符并将其转成如上图所示的电路。二进制的加法运算和十进制的加法相似,十进制是逢十进一,而二进制是逢二进一。二进制加法的基本运算如下:
0 + 0 = 0;
0 + 1 = 1;
1 + 0 = 1;
1 + 1 = 10;
两位的二进制加法
11 + 1 = 100;
11 + 11 = 110;
…
5.3.2 减法运算符
减法运算符,在Verilog代码中可以直接使用符号“-”:
|
1 |
assign C=A - B; |
其电路示意图如下所示:

图1.3- SEQ 图1.3- * ARABIC11减法电路示意图
综合器可以识别减法运算符并将其直接转成上图所示的电路。
二进制的减法运算和十进制的减法运算是相似的,也有借位的概念。十进制是借一当十,二进制则是借一当二。1位减法基本运算如下:
0 - 0 = 0;
0 - 1 = 1,同时需要借位;
1 - 0 = 1;
1 - 1 = 0 ;
5.3.3 乘法运算符
乘法运算符,在Verilog代码中可以直接使用符号“*”:
|
1 |
assign C=A * B; |
其电路示意图如下所示:

图1.3- SEQ 图1.3- * ARABIC12乘法电路示意图
综合器可以识别乘法运算符,将其直接转成上图所示的电路。二进制的乘法运算和十进制的乘法运算是相似的,其计算过程是相同的。1位乘法基本运算如下:
0 * 0 = 0;
0 * 1 = 0;
1 * 0 = 0;
1 * 1 = 1;
多位数之间相乘,与十进制计算过程也是相同的。例如2’b11 * 3’b101的计算过程如下:
|
|
|
|
1 |
1 |
|
X |
|
1 |
0 |
1 |
|
|
|
|
1 |
1 |
|
|
|
0 |
0 |
|
|
|
1 |
1 |
|
|
|
= |
1 |
1 |
1 |
1 |
5.3.4 除法和求余运算符
除法运算符,可以在Verilog代码中直接使用符号“/”,而求余运算符是“%”:
|
1 2 |
assign C=A / B; assign D = A%B; |
除法的电路示意图如下所示:

图1.3- SEQ 图1.3- * ARABIC13除法电路示意图
求余的电路示意图如下所示:

图1.3- SEQ 图1.3- * ARABIC14求余电路示意图
综合器可以识别除法运算符和求余运算符,但是这两种运算符包括大量的乘法、加法和减法操作,所以在FPGA里除法器的电路是非常大的,综合器可能无法直接转成上图所示的电路。
此处可能存在疑虑:为什么除法和求余会占用大量的资源呢?可以来分析一下十进制除法和求余的过程,以122除以11为例。
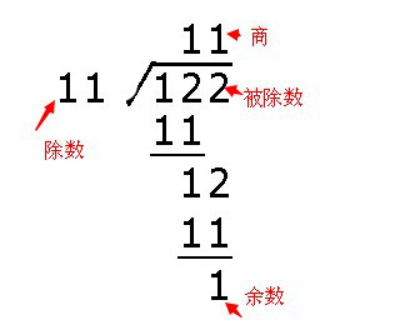
图1.3- SEQ 图1.3- * ARABIC15十进制除法和求余过程
在做上面运算的过程中涉及到多次的移位、乘法、减法等运算。也就是说进行一次除法运算使用到了多个乘法器、减法器,需要比较大的硬件资源,二进制运算也是同样的道理。
所以,在设计代码中,一般不使用除法和求余。在算法中会想各种办法来避免除法和求余操作。因此在数字信号处理、通信、图像处理中会发现有大量的乘法、加减法等,却很少看到除法和求余运算。但在仿真测试中是可以使用除法和求余的,因为其只是用于仿真测试而不用综合成电路,自然也就不需要关心占用多少资源了。
5.3.5 经验总结
Ø 位宽问题
在写代码时,需要注意信号的位宽,最终的结果取决于“=”号左边信号的位宽,保存低位,丢弃高位。例如:
|
1 2 3 4 5 6 7 8 |
wire c; wire[1:0] d; wire[2:0] e; wire[2:0] f; assign c = 1’b1 + 1’b1; assign d = 1’b1 + 1’b1; assign e = 1’b1 + 1’b1; assign f = 1 + 1; |
信号c的位宽为1位,所以运算的结果最终保留最低1位,因此c的值为1’b0。由于d的位宽有2位,所以运算的结果可以保留低2位,因此d的值为2’b10。由于e的位宽有3位,所以运算的结果可以保留低3位,因此e的值为3’b010。“1”默认是32位,1+1的结果也是32位,但由于f的位宽只有3位,所以运算的结果可以保留低3位,因此f的值为3’b010。
减法运算也是相同的道理,以如下代码为例:
|
1 2 3 4 5 6 7 8 |
wire c; wire[1:0] d; wire[2:0] e; wire[3:0] f; assign c = 0 -1 ; assign d = 0 - 1 ; assign e = 0 -1 ; assign f = 0 - 1; |
“0-1”得到的二进制值是“1111111111….”,但保存结果取决于“=”号左边信号的位宽。c的位宽是1,保留最低1位,所以c的值为1’b1。由于d的位宽有2位,结果保留低2位,所以d的值为2’b11。由于e的位宽有3位,结果保留低3位,所以e的值为3’b111。f的位宽有4位,所以运算的结果可以保留低4位,所以f的值为4’b1111。
在写乘法代码时,同样需要注意信号的位宽,最终的结果取决于“*”号左边信号的位宽,保存低位,丢弃高位:
|
1 2 3 4 5 6 7 8 9 10 |
wire c; wire[1:0] d; wire[2:0] e; wire[3:0] f; wire[4:0] h; assign c = 2’b11 * 3’b101 ; assign d = 2’b11 * 3’b101 ; assign e = 2’b11 * 3’b101 ; assign f = 2’b11 * 3’b101; assign h = 2’b11 * 3’b101; |
“2’b11 * 3’b101”得到的二进制值是“4’b1111”,但保存结果取决于“*”号左边信号的位宽。c的位宽是1,保留最低1位,所以c的值为1’b1。由于d的位宽有2位,结果保留低2位,所以d的值为2’b11。由于e的位宽有3位,结果保留低3位,所以e的值为3’b111。f的位宽有4位,所以运算的结果可以保留低4位,所以f的值为4’b1111。需要注意的是h,该信号有5位,4’b1111赋给5位信号,结果是高位补0,所以其结果为5’b01111。
Ø 补码的由来
FPGA实现各种算法的时候,首要的就是保证运算结果的正确性,否则一切毫无意义。在分析加加法运算符和减法运算符的时候可以发现保存结果的信号位宽是否合理对正确性与否有很大的影响。
例如下面的加法运算:
表1.3- SEQ 表1.3- * ARABIC5加法运算结果
|
运算 |
十进制 结果 |
运算 |
十进制 结果 |
|
|
1位加法运算,1位保存结果,不保存进位 |
||||
|
1’b0 + 1’b0 = 1’b0 |
0 |
1’b1 + 1’b0 = 1’b1 |
1 |
|
|
1’b0 + 1’b1 = 1’b1 |
1 |
1’b1 + 1’b1 = 1’b0 |
0 |
|
|
1位加法运算,2位保存结果,保存进位 |
||||
|
1’b0 + 1’b0 = 2’b0 |
0 |
1’b1 + 1’b0 = 2’b01 |
1 |
|
|
1’b0 + 1’b1 = 2’b1 |
1 |
1’b1 + 1’b1 = 2’b10 |
2 |
|
|
1位数 + 2位数,2位保存结果,不保存进位 |
||||
|
1’b0 + 2’b00 = 2’b00 |
0 |
1’b1 + 2’b00 = 2’b01 |
1 |
|
|
1’b0 + 2’b01 = 2’b01 |
1 |
1’b1 + 2’b01 = 2’b10 |
2 |
|
|
1’b0 + 2’b10 = 2’b10 |
2 |
1’b1 + 2’b10 = 2’b11 |
3 |
|
|
1’b0 + 2’b11 = 2’b11 |
3 |
1’b1 + 2’b11 = 2’b00 |
0 |
|
|
1位数 + 2位数,3位保存结果,保存进位 |
||||
|
1’b0 + 2’b00 = 3’b000 |
0 |
1’b1 + 2’b00 = 3’b001 |
1 |
|
|
1’b0 + 2’b01 = 3’b001 |
1 |
1’b1 + 2’b01 = 3’b010 |
2 |
|
|
1’b0 + 2’b10 = 3’b010 |
2 |
1’b1 + 2’b10 = 3’b011 |
3 |
|
|
1’b0 + 2’b11 = 3’b011 |
3 |
1’b1 + 2’b11 = 3’b100 |
4 |
|
从上表可以发现,如果不保留进位,当加法出现进位的时候计算的结果是不正确的,只有保留了进位计算的结果才是正确的。由此可以得出一个结论:使用加法的时候,为了保证结果的正确性,必须保存进位,也就是结果要扩展位宽。
例如两个8位的数相加,则结果要扩展一位,将位宽设定为9位。
|
1 2 3 4 5 |
wire[7:0] a,b; wire[7:0] c ; wire[8:0] d ; assign c = a + b; //结果不正确 assign d = a + b; //结果正确 |
接着再来分析一下减法运算,如下表所示例子:
表1.3- SEQ 表1.3- * ARABIC6减法运算结果
|
运算 |
十进制 结果 |
运算 |
十进制 结果 |
|
2位减法运算,2位保存结果 |
|||
|
2’b00 - 2’b00 = 2’b00 |
0 |
2’b10 - 2’b00 = 2’b10 |
2 |
|
2’b00 - 2’b01 = 2’b11 |
3 |
2’b10 - 2’b01 = 2’b01 |
1 |
|
2’b00 - 2’b10 = 2’b10 |
2 |
2’b10 - 2’b10 = 2’b00 |
0 |
|
2’b00 - 2’b11 = 2’b01 |
1 |
2’b10 - 2’b11 = 2’b11 |
3 |
|
2’b01 - 2’b00 = 2’b01 |
1 |
2’b11 - 2’b00 = 2’b11 |
3 |
|
2’b01 - 2’b01 = 2’b00 |
0 |
2’b11 - 2’b01 = 2’b10 |
2 |
|
2’b01 - 2’b10 = 2’b11 |
3 |
2’b11 - 2’b10 = 2’b01 |
1 |
|
2’b01 - 2’b11 = 2’b10 |
2 |
2’b11 - 2’b11 = 2’b00 |
0 |
注意表中和2’b00-2’b01,结果是2’b11,对应的十进制值为3,但期望的结果是“-1”。同样的道理,2’b01 - 2’b11,结果是2’b10,对应的十进制值为2,而期望的结果是“-2”,所以上面的结果是不正确的。
当期望结果中有正负之分时,可以通过增加一个符号位来区别结果的正负。业内约定的表示方法为,最高位为0时表示正数,最高位值为1表示负数。符号位之后的数值用低2位表示,结果如下表:
表1.3- SEQ 表1.3- * ARABIC7增加符号位的减法运算结果
|
运算 |
十进制 结果 |
运算 |
十进制 结果 |
|
2位减法运算,3位保存结果,其中最高位是符号位 |
|||
|
2’b00 - 2’b00 = 3’b000 |
+0 |
2’b10 - 2’b00 = 3’b010 |
+2 |
|
2’b00 - 2’b01 = 3’b111 |
-3 |
2’b10 - 2’b01 = 3’b001 |
+1 |
|
2’b00 - 2’b10 = 3’b110 |
-2 |
2’b10 - 2’b10 = 3’b000 |
+0 |
|
2’b00 - 2’b11 = 3’b101 |
-1 |
2’b10 - 2’b11 = 3’b111 |
-3 |
|
2’b01 - 2’b00 = 3’b001 |
+1 |
2’b11 - 2’b00 = 3’b011 |
+3 |
|
2’b01 - 2’b01 = 3’b000 |
+0 |
2’b11 - 2’b01 = 3’b010 |
+2 |
|
2’b01 - 2’b10 = 3’b111 |
-3 |
2’b11 - 2’b10 = 3’b001 |
+1 |
|
2’b01 - 2’b11 = 3’b110 |
-2 |
2’b11 - 2’b11 = 3’b000 |
+0 |
从上表中可以看出增加符号位后还是会存在部分运算结果与预期不符合的问题。例如表中的2’b00-2’b01,结果是3’b111,对应的十进制值为-3,但期望的结果是“-1”。所以上面的结果仍然是不正确的。
现在,重新对二进制数“000~111”进行如下转换:
a. 正数:保持不变
b. 负数:符号位保持不变,数值取反加1。
也就是说,如果是正数“+1”,之前是用“001”表示,现在仍然是用“001”表示。如果是负数“-1”,之前是用“101”表示,现在则是用“111”表示。负数“-3”,之前是用“111”表示,现在则是用“101”表示。这种表示方式就是补码表示方式。
改为用补码来表示后,再来分析下结果:
表1.3- SEQ 表1.3- * ARABIC8补码表示减法运算结果
|
运算 |
补码 结果 |
运算 |
补码 结果 |
|
2位减法运算,3位保存结果,其中最高位是符号位 |
|||
|
2’b00 - 2’b00 = 3’b000 |
+0 |
2’b10 - 2’b00 = 3’b010 |
+2 |
|
2’b00 - 2’b01 = 3’b111 |
-1 |
2’b10 - 2’b01 = 3’b001 |
+1 |
|
2’b00 - 2’b10 = 3’b110 |
-2 |
2’b10 - 2’b10 = 3’b000 |
+0 |
|
2’b00 - 2’b11 = 3’b101 |
-3 |
2’b10 - 2’b11 = 3’b111 |
-1 |
|
2’b01 - 2’b00 = 3’b001 |
+1 |
2’b11 - 2’b00 = 3’b011 |
+3 |
|
2’b01 - 2’b01 = 3’b000 |
+0 |
2’b11 - 2’b01 = 3’b010 |
+2 |
|
2’b01 - 2’b10 = 3’b111 |
-1 |
2’b11 - 2’b10 = 3’b001 |
+1 |
|
2’b01 - 2’b11 = 3’b110 |
-2 |
2’b11 - 2’b11 = 3’b000 |
+0 |
可以看到上表的结果全部都是正确的,与预期全部一致。这一过程虽然完全没有对代码进行任何改变,但通过更改数据的定义就实现了正确的结果。
在之前的讨论中,加数、被加数、减数和被减数的运算过程都没有使用有符号数。现在使用有符号数的补码重新对其进行表示。假设加数、被加数、减数和被减数都是2位(范围为-2~1),考虑到进位和借位原因,结果用3位来表示(范围为-4~3)。因为结果位宽变为3位,所以减数和被减数都扩展成用3位表示,列出下表:
表1.3- SEQ 表1.3- * ARABIC9补码表示运算结果
|
十进制运算 |
二进制补码表示 |
补码 结果 |
|
0-0 |
3’b000 - 3’b000 = 3’b000 |
+0 |
|
0-1 |
3’b000 - 3’b001 = 3’b111 |
-1 |
|
0-(-2) |
3’b000 - 3’b110 = 3’b010 |
+2 |
|
0-(-1) |
3’b000- 3’b111 = 3’b001 |
+1 |
|
1-0 |
3’b001 - 3’b000 = 3’b001 |
+1 |
|
1-1 |
3’b001 - 3’b001 = 3’b000 |
+0 |
|
1-(-2) |
3’b001 - 3’b110 = 3’b011 |
+3 |
|
1-(-1) |
3’b001 - 3’b111 = 3’b110 |
+2 |
|
-2-0 |
3’b110 - 3’b000 = 3’b110 |
-2 |
|
-2-1 |
3’b110 - 3’b001 = 3’b101 |
-3 |
|
-2-(-2) |
3’b110 - 3’b110 = 3’b000 |
+0 |
|
-2-(-1) |
3’b110 - 3’b111 = 3’b111 |
-1 |
|
-1-0 |
3’b111 - 3’b000 = 3’b111 |
-1 |
|
-1-1 |
3’b111 - 3’b001 = 3’b110 |
-2 |
|
-1-(-2) |
3’b111 - 3’b110 = 3’b001 |
+1 |
|
-1-(-1) |
3’b111 - 3’b111 = 3’b000 |
+0 |
|
0+0 |
3’b000 + 3’b000 = 3’b000 |
+0 |
|
0+1 |
3’b000 + 3’b001 = 3’b001 |
+1 |
|
0+(-2) |
3’b000 + 3’b110 = 3’b110 |
-2 |
|
0+(-1) |
3’b000 + 3’b111 = 3’b111 |
-1 |
|
1+0 |
3’b001 + 3’b000 = 3’b001 |
+1 |
|
1+1 |
3’b001 + 3’b001 = 3’b010 |
+2 |
|
1+(-2) |
3’b001 + 3’b110 = 3’b111 |
-1 |
|
1+(-1) |
3’b001 + 3’b111 = 3’b000 |
+0 |
|
-2+0 |
3’b110 + 3’b000 = 3’b110 |
-2 |
|
-2+1 |
3’b110 + 3’b001 = 3’b111 |
-1 |
|
-2+(-2) |
3’b110 + 3’b110 = 3’b100 |
-4 |
|
-2+(-1) |
3’b110 + 3’b111 = 3’b101 |
-3 |
|
-1+0 |
3’b111 + 3’b000 = 3’b111 |
-1 |
|
-1+1 |
3’b111 + 3’b001 = 3’b000 |
+0 |
|
-1+(-2) |
3’b111 + 3’b110 = 3’b101 |
-3 |
|
-1+(-1) |
3’b111 + 3’b111 = 3’b110 |
-2 |
总结运算步骤如下:
1. 根据“人的常识”,预计结果的最大最小值,从而确定结果的信号位宽。
2. 将加数、减数等数据,位宽扩展成结果位宽一致。
3. 按二进制加减法进行计算。
通过以上方式,得到的就是补码的结果。事实上,在FPGA甚至计算机系统中,所有数据的保存的方式都是补码的形式。如果想要了解更多关于补码的内容可以参阅相关资料。
5.4 逻辑运算符
|
类型 |
情况 |
功能 |
verilog代码 |
电路示意图 |
备注 |
|
与门 |
1位逻辑与(符号:&&) |
A和B都为1,C为1;否则C为0。 |
reg A,B; always@(*)begin C=A&&B; end |
|
注意:FPGA支持多输入的与门,例如四输入与门,输入可为ABCD,输出为E,当ABCD同时为1时,E为1 |
|
多位逻辑与(符号:&&) |
A或B都不为0时,C为1,否则为0。 |
reg[2:0] A,B,C; always@(*)begin C=A&&B; end |
|
多位信号之间的逻辑与,很容易引起歧义,设计最好不要用多位数的逻辑与。如果要实现上面功能,建议代码改为如下: always@(*)begin C=(A!=0)&&(B!=0); end |
|
|
或门 |
1位逻辑或(符号:||) |
A和B其中1个为1,C为1;否则C为0。 |
reg A,B; always@(*)begin C=A||B; end |
|
注意:FPGA支持多输入的与门,例如四输入与门,输入可为ABCD,输出为E,当ABCD同时为1时,E为1 |
|
多位逻辑或(符号:||) |
A和B其中1个非0,C为1;否则C为0。 |
reg[2:0] A,B,C; always@(*)begin C=A||B; end
|
|
多位信号之间的逻辑或,很容易引起歧义。最好不要用多位的逻辑或。如果要实现相同功能,建议改为如下: always@(*)begin C=(A!=0)||(B!=0); end |
在Verilog HDL语言中存在3种逻辑运算符,它们分别是:
(1)&&:逻辑与;
(2) | | :逻辑或;
(3)!:逻辑非。
5.4.1 逻辑与
“&&”是双目运算符,其要求有两个操作数,如a && b。
(1)1位逻辑与
|
1 2 3 4 |
reg A,B; always@(*)begin C=A&&B; end |
A和B都为1时,C为1,否则C为0。
对应硬件电路图如下所示:
图1.3- SEQ 图1.3- * ARABIC161位逻辑与硬件电路
(2)多位逻辑与
|
1 2 3 4 |
reg[2:0] A,B,C; always@(*)begin C=A&&B; end |
100= 3A或B都不为0时,C为1,否则为0。
对应硬件电路图如下所示:
图1.3- SEQ 图1.3- * ARABIC17多位逻辑与硬件电路
5.4.2 逻辑或
“||”是双目运算符,其要求有两个操作数,如 a||b。
(1)1位逻辑或
|
1 2 3 4 |
reg A,B; always@(*)begin C=A||B; end |
A和B其中1个为1,C为1,否则C为0。
对应硬件电路图如下图所示:
图1.3- SEQ 图1.3- * ARABIC181位逻辑或硬件电路
(2)多位逻辑或
|
1 2 3 4 |
reg[2:0] A,B,C; always@(*)begin C=A||B; end |
A和B其中1个非0,C为1,否则C为0。
对应硬件电路图如下图所示:
图1.3- SEQ 图1.3- * ARABIC19多位逻辑或硬件电路
5.4.3 逻辑非
“!”是单目运算符,只要求有一个操作数,如!(a>b)。
|
1 2 3 4 |
if ( !a ) begin { } end |
对操作数a需要先判断非a是否为真,为真就执行{}内的操作,为假的话就结束操作。
下表为逻辑运算的真值表,其表示当a和b的值为不同的组合时各种逻辑运算所得到的值。
表1.3- SEQ 表1.3- * ARABIC10逻辑运算的真值表
|
a |
b |
! a |
! b |
a&&b |
a| |b |
|
真 |
真 |
假 |
假 |
真 |
真 |
|
真 |
假 |
假 |
真 |
假 |
真 |
|
假 |
真 |
真 |
假 |
假 |
真 |
|
假 |
假 |
真 |
真 |
假 |
假 |
逻辑运算符最后的结果只有逻辑真或逻辑假两种,即1或0。一般情况下用逻辑运算符作判断条件时逻辑与操作只能是两个1位宽的数,只有两个表达式同时为真才为真,有一个为假则为假。
如果操作数是多位的,则可以将操作数看做整体,若操作数中每一位都是0值则为逻辑0值;若操作数中有1则为逻辑1值。
|
1 2 3 |
assign a = 4’b0111 && 4’b1000; assign b = 4’b0111 || 4’b1000; assign c = !4’b0111; |
由于4’b0111和4’b1000都不是0,不为0则被认为是逻辑真,所以上面的代码等效于如下代码。
|
1 2 3 |
assign a = 1’b1 && 1’b1; assign b = 1’b1 || 1’b1; assign c = !(1’b1); |
也就是结果为a为逻辑真,b为逻辑真,c为逻辑假。
5.4.4 经验总结
Ø 逻辑运算符的优先级
逻辑运算符中“&&”和“||”的优先级低于算数运算符;“!”的优先级高于双目逻辑运算符。
举例如下:
|
(a < b)&&(c > d)可写成:a < b && c > d ; (a = = b)| |(c = = d)可写成:a = = b | | c = = d ; (!a)| |(a > b)可写成:!a | | a > b 。 |
Ø 逻辑运算符两边对应的是1比特信号
使用心得:逻辑运算符两边对应的是1比特信号
|
1 2 |
wire[3:0] a, b; assign d = a &&b ; |
注意上文代码,其中a和b都是多比特信号,表示两个多比特信号进行逻辑与。这句代码的正确理解是:当a不等于0 并且 b不等于0时,d的值为1。然而即使是有过多年工作经验的工程师也很难从直观上直接理解上文代码所隐含的意思。不等于0就是表示逻辑真,等于0就表示逻辑假的这一概念很容易被忽略。
因此上文代码,虽然从功能上没有错误,但设计师在设计中不应该以炫耀技术为目的进行代码编写,而且这种写法很容易出现误设计的情况,例如可能原本要表达 assign d =a & b,但最后由于设计不够直观而写成了上面的代码,导致设计出现问题。因此在设计中写出直观能理解,让自己与他者看到代码时可以立刻明白代码的意思非常重要,所以建议上面代码写成如下形式。
|
1 2 |
wire[3:0] a, b; assign d = (a!=0) && (b!=0) ; |
Ø 多用括号区分优先级
使用心得2:不要试图记住优先级,而是要多用括号
实际上,工程师们在工作中并不会记住所有优先级排序,记住所有的优先级的这一工作也并不会大幅度的提升工程师的工作效率。在设计中可能会遇到如下所示代码:
(1)a < b && c > d ;
(2)a = = b | | c = = d ;
(3)!a | | a > b 。
假如没有记住运算符的优先级,遇到类似这三个例子的情况时势必会花一定的时间来理清思路,思考究竟先判断哪部分。假如工程师能够记住优先级,也需要就这些代码进行沟通和检查的工作,而且人是容易犯错的,而这些错误经常会被忽略,很难被检查出来。
因此,为了提高程序的可读性,明确表达各运算符间的优先关系,建议在设计时多使用括号。上面的三个例子就可分别写成:
1)(a < b)&&(c > d);
2)(a = = b)| |(c = = d);
3)(!a)| |(a > b)。
Ø 少用逻辑非
使用心得3:多用“逻辑与”和“逻辑或”,少用逻辑非
“逻辑与”翻译成中文就是“并且”,“逻辑或”翻译成中文就是“或者”。假设有一个信号flag,0表示空闲,1表示忙。“(!(flag==0) && a==4’b1000)”,读起来就是“在空闲的时候取其反状态,并且当a等于4’b1000时条件成立”。这样读起来非常拗口,并且在阅读这一代码时还需要脑袋还要多转一下弯,多进行一层思考。为了让代码更加直观,建议上面的例子写成“flag==1 && a==4’b1000”,读起来就是“在忙并且 a等于4’b1000的时候”条件成立。
5.5 按位逻辑运算符
|
类型 |
情况 |
功能 |
verilog代码 |
电路示意图 |
备注 |
|
反相器
|
1位反相器 (符号:~) |
将值取反 |
reg A,B; always@(*)begin B=~A; end |
|
|
|
多位反相器(符号:~) |
将值取反 |
reg[1:0] A,B; always@(*)begin B=~A; end |
|
如果A和B都是n位,实际电路就是有n个反相器。画电路图时可画一个来简化。 |
|
|
按位与(符号:&) 常用1 |
A和B对应的比特分别相与。 |
reg[2:0] A,B,C; always@(*)begin C=A&B; end |
|
|
|
|
按位与 (符号:&) 常用2 |
A的各位之间相与。 |
reg[2:0] A; always@(*)begin C=&A; end |
|
|
|
|
或门 |
1位逻辑或 (符号:||) |
A和B其中1个为1,C为1;否则C为0。 |
reg A,B; always@(*)begin C=A||B; end |
|
注意: FPGA支持多输入的与门,例如四输入与门,输入可为ABCD,输出为E,当ABCD同时为1时,E为1 |
|
按位或 (符号:|) 常用1 |
A和B对应的比特相或。 |
reg[2:0] A,B,C; always@(*)begin C=A|B; end
|
|
|
|
|
按位或 (符号:|) 常用2 |
A的各位之间相或 |
reg[2:0] A; always@(*)begin C=|A; end
|
|
|
注:~ ^, ^ ~(二元异或非即同或):(相当于同或门运算)。
在Verilog HDL语言中有下面几种按位运算符:
~(一元非):(相当于非门运算)
&(二元与):(相当于与门运算)
|(二元或):(相当于或门运算)
^(二元异或):(相当于异或门运算)
这些操作符在输入操作数的对应位上按位操作,并产生向量结果。下图各真值表种显示对于不同按位逻辑运算符按位操作的结果:
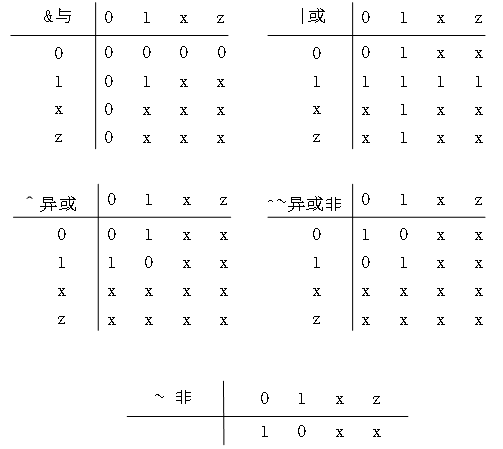
图1.3- SEQ 图1.3- * ARABIC20按位逻辑运算符真值表
5.5.1 单目按位与
单目按位与运算符&,运算符后为需要进行逻辑运算的信号,表示对信号进行每位之间相与的操作。例如
Reg[3:0] A,C;
assign C=&A;
上面代码等价于 C = A[3] & A[2] & A[1] & A[0];
如果A=4’b0110,C的结果为0。
5.5.2 单目按位或
单目按位或运算符|,运算符后为需要进行逻辑运算的信号,表示对信号进行每位之间相或的操作。例如
reg[3:0] A,C;
assign C=|A;
上面代码等价于 C = A[3] | A[2] | A[1] | A[0];
如果A=4’b0110,C的结果为1。
5.5.3 单目按位非
单目按位非运算符~,运算符后为需要进行逻辑运算的信号,表示对信号进行每位取反的操作。例如
reg[3:0] A,C;
assign C=~A;
上面代码等价于 C[3] = ~A[3],C[2] = ~A[2],C[1] = ~A[1],C[0] = ~A[0]。
如果A=4’b0110,C的结果为4’b1001。
5.5.4 双目按位与
双目按位与运算符&,信号位于运算符的左右两边,表示的是对这两个信号进行对应位相与的操作。例如
reg[3:0] A,B,C;
assign C = A & B;
上面的代码等价于:C[0] = A[0] & B[0],C[1] = A[1] & B[1],C[2] = A[2] & B[2],C[3] = A[3] & B[3]。如果A=4’b0110,B=4’b1010,C的结果为4’b0010。
如果操作数长度不相等, 长度较小的操作数在最左侧添0 补位。例如,
reg[1:0] A;
reg[2:0] B;
reg[3:0] C;
assign C = A & B;
上面的代码等价于:C[0] = A[0] & B[0],C[1] = A[1] & B[1],C[2] = 0& B[2],C[3] = 0 &0。
5.5.5 双目按位或
双目按位或运算符|,信号位于运算符的左右两边,表示的是对这两个信号进行对应位相或的操作。例如
reg[3:0] A,B,C;
assign C = A | B;
上面的代码等价于:C[0] = A[0] | B[0],C[1] = A[1] | B[1],C[2] = A[2] | B[2],C[3] = A[3] | B[3]。如果A=4’b0110,B=4’b1010,C的结果为4’b1110。
如果操作数长度不相等, 长度较小的操作数在最左侧添0 补位。例如,
reg[1:0] A;
reg[2:0] B;
reg[3:0] C;
assign C = A | B;
上面的代码等价于:C[0] = A[0] | B[0],C[1] = A[1] | B[1],C[2] = 0 | B[2],C[3] = 0 | 0。
5.5.6 双目按位异或
双目按位异或运算符^,信号位于运算符的左右两边,表示的是对这两个信号进行对应位相异或的操作。异或是指0^0=0,1^1=0,0^1=1,即相同为0,不同为1。例如
reg[3:0] A,B,C;
assign C = A ^ B;
上面的代码等价于:C[0] = A[0] ^ B[0],C[1] = A[1] ^ B[1],C[2] = A[2] ^ B[2],C[3] = A[3] ^ B[3]。如果A=4’b0110,B=4’b1010,C的结果为4’b1100。
如果操作数长度不相等, 长度较小的操作数在最左侧添0 补位。例如,
reg[1:0] A;
reg[2:0] B;
reg[3:0] C;
assign C = A | B;
上面的代码等价于:C[0] = A[0] ^ B[0],C[1] = A[1] ^ B[1],C[2] = 0 ^ B[2],C[3] = 0 ^ 0。
5.5.7 经验总结
Ø 逻辑运算符和位运算符的区别
逻辑运算符包括&&、||、!,位运算符包括&、|、~。那么逻辑运算符和位运算符有什么区别呢?
将逻辑与“&&”和按位与“&”进行对比可以看出,逻辑与运算符的运算只有逻辑真或逻辑假两种结果,即1或0;而“&”是位运算符,用于两个多位宽数据操作。对于位运算符操作,两个数按位进行相与、相或或者非。
|
1 2 3 4 5 6 |
assign a = 4’b0111 && 4’b1000; assign b = 4’b0111 || 4’b1000; assign c = !4’b0111; assign d = 4’b0111 & 4’b1000; assign e = 4’b0111 | 4’b1000; assign f = ~4’b0111; |
上面运行的结果为:a=1’b1,b=1’b1,c=1’b0,d=4’b000,e=4’b1111,f=4’b1000。
5.6 关系运算符
|
分类 |
情况 |
功能 |
代码 |
电路示意图 |
|
|
比较器 |
相等 |
相等则为1 |
always@(*)begin if(A==B) C=1; else C=0; end |
|
|
|
大于 |
大于则为1 |
always@(*)begin if(A>B) C=1; else C=0; end |
|
|
|
|
大于 等于 |
大于等于则为1 |
always@(*)begin if(A>=B) C=1; else C=0; end |
|
|
|
|
小于 |
小于则为1 |
always@(*)begin if(A<B) C=1; else C=0; end |
|
|
|
|
小于 等于 |
小于等于则为1 |
always@(*)begin if(A<=B) C=1; else C=0; end |
|
|
关系运算符有:>(大于)、<(小于)、>=(不小于)、<=(不大于)、== (逻辑相等)和!= (逻辑不等)。
关系操作符的结果为真(1)或假(0)。如果操作数中有一位为x或z,那么结果为x。例:
23 > 45 :结果为假(0 )。
52 < 8'hxFF:结果为x 。
如果操作数长度不同,长度较短的操作数在最重要的位方向(左方)添0 补齐。例如:
'b1000 > = 'b01110 等价于:'b01000 > = 'b01110,结果为假(0)。
在逻辑相等与不等的比较中,只要一个操作数含有x 或z,比较结果为未知(x),如假定Data = 'b11x0; Addr = 'b11x0; 那么Data == Addr,比较结果不定,即结果为x 。
5.7 移位运算符
在Verilog HDL中有两种移位运算符,分别为“<<”(左移位运算符)和“>>”(右移位运算符)。下面分别介绍两者的用法:
|
情况 |
功能 |
verilog代码 |
电路示意图 |
备注 |
|
移位 (右移:>> 左移:<<) |
A向右或向左移动后,赋值给B |
reg[3:0] A; reg[2:0] B; always@(*)begin B=A>>2; end |
|
移位操作,实际上是选哪线相连。 |
5.7.1 左移运算符
在Verilog HDL中,用“<<”表示左移运算符。其一般表达式为:
A << n;
其中,A代表要进行移位的操作数,n代表要左移多少位。此表达式的意义是把操作数A左移n位。左移操作属于逻辑移位,需要用0来填补移出的空位,即在低位补0。左移n位,就要补n个0。
|
1 2 |
wire[3:0] a; assign a = 4’b0111<< 2; |
以上代码由于左移了2位,所以在低位补2个零,所以上面代码运行结果是:a = 4’b1100。
左移操作中有以下三点值得注意的地方:
(1)左移操作是不消耗逻辑资源的,甚至连与门、非门都不需要,它只是线的连接。
|
1 2 3 |
wire[3:0] c; wire[3:0]b; assign c = b << 2; |
上面代码是将信号b左移两位并赋给c,其所对应的硬件电路如下图:

图1.3- SEQ 图1.3- * ARABIC21左移对应的硬件电路
(2)左移操作需根据位宽储存结果
在学习过程中可能看到过如下代码:
4’b1001<<1=4’b0010与4’b1001<<1=5’b10010
为什么操作数同样是4’b1001,都是左移一位,但结果一个是4’b0010,一个是5’b10010呢?
这是因为左移操作后,要看用多少位来存储结果。
|
1 2 3 |
wire[3:0] a; assign b = 4’b1001; assign a = b << 1; |
上面代码中由于a是4比特,只能保存4位结果,所以b左移1位赋给4 bit的a,用0填补移出的位后结果为a = 4’b0010 ;
|
1 2 3 4 |
wire[4:0] a; assign b = 4’b1001; assign a = b << 1; a=10010; |
而上面代码中由于a是5比特,能保存5位结果,所以b左移1位赋给5 bit的a,用0填补移出的位后结果为a = 5’b10010 ;
(3)左移操作的操作数可以是常数,也可以是信号。同样,左移操作的移位数、常数也可以是信号。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
reg[4:0] a; reg[2:0] cnt; always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin cnt<= 0; end else begin cnt<= cnt + 1; end end always @(*)begin a = 4'b1 <<cnt; end |
上面代码中cnt每个时钟加1,由于是3比特,所以值为0~2。a则是4’b1左移cnt位。当cnt等于0时左移0位,a等于4’b1;当cnt等于1时左移1位,a等于4’b10。以此类推,a的每个时钟变化情况如下所示:

图1.3- SEQ 图1.3- * ARABIC22信号随时钟变化情况
需要注意的是,当移位数是信号时,其综合的电路并不是简单的连线,可能会综合出如下图所示的选择器。然而即便如此,这种硬件电路所消耗的资源依然比较少。

图1.3- SEQ 图1.3- * ARABIC23移位数为变量时会综合出选择器
5.7.2 右移运算符
在Verilog HDL中,用“>>”表示右移运算符。其一般表达式为:
A >>n;
其中,A代表要进行移位的操作数,n代表要右移多少位。此代码表示的意义是把操作数A右移n位。
在右移操作中有以下三点值得注意的地方:
(1)右移操作属于逻辑移位,需要用0来填补移出的空位,即在高位补0,补多少个0,取决于保存结果的信号的位宽。
|
1 2 |
wire[5:0] a; assign a = 4’b0111<< 2; |
4’b0111右移两位后的结果为2’b01,由于a是6位的,2位赋值给6位需要在高位补0,因此需要补4个0。所以上面代码运行结果是:
a = 6’b0001
(2)与左移操作相似,右移操作是不消耗逻辑资源的,甚至连与门、非门都不需要,其只是线的连接。
|
1 2 3 |
wire[3:0] a; wire[3:0] b; assign a = b >> 2; |
上面代码是将信号b左移两位并赋给a,其所对应的硬件电路如下图所示。

图1.3- SEQ 图1.3- * ARABIC24右移对应的硬件电路
(3)左移操作的操作数可以是常数,也可以是信号。同样,右移操作的移位数可以是常数,也可以是信号。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
reg[4:0] a; reg[2:0] cnt; always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin cnt<= 0; end else begin cnt<= cnt + 1; end end always @(*)begin a = 4'b1000>>cnt; end |
上面代码中,cnt每个时钟加1,由于是3比特,所以值为0~2。a则是4’b1000右移cnt位。当cnt等于0时右移0位,a等于4’b1000;当cnt等于1时右移1位,a等于4’b0100。以此类推,a的每个时钟变化情况如下图所示。

图1.3- SEQ 图1.3- * ARABIC25信号随时钟变化情况
与左移操作类似,在右移操作中,如果移位数是信号时,其综合的电路就不是简单的连线,而是有可能会综合出如下图所示的选择器。然而同样在这一情况下,这种硬件电路所消耗的资源依然比较
少。

图1.3- SEQ 图1.3- * ARABIC26移位数为变量时会综合出选择器
5.7.3 经验总结
Ø 通过左移乘法运算
FPGA中要尽量避免乘法运算,因为这种计算需要占用较大的硬件资源,并且运算速度较慢。当不得不使用乘法的时候,尽量乘以2的N次方,这样在设计中可以利用左移运算来实现该乘法运算,从而大大减少硬件资源。
当乘数是2的N次方的常数时可以用移位运算来实现乘法。例如:a*2,等价于 a<<1;a*4等价于a<<2;a*8等价于a<<3,依此类推。
即使乘数不是2的N次方的常数,也可以通过移位运算来简化实现。例如:
|
1 2 |
assign b = a*127; assign c = (a<<7) –a; |
上面代码中b和c都可以实现a*127,但第1行消耗了一个乘法,而第2行则只用到一个减法器。
|
1 2 |
assign b = a*67; assign c = (a<<6) +(a<<1) +a; |
上面代码中,b和c都可以实现a*67,但第1行消耗了一个乘法,而第2行则只用到两个加法器,从而节省了资源。
可以注意到,上面两个例子中的乘数都是常数,那么在设计时这种乘法也要花时间和精力来考虑优化吗?其实是不必要的,因为现在综合工具都很强大,当工具发现乘数是常数时会自动按上述过程进行优化,也就是说乘以常数在实质上并不消耗乘法器资源,可以放心使用。
但当出现乘数不是常数的情况时就要注意乘法的使用了。尽量将信号转换为与2的N次方相关的形式。例如当数据要扩大后来计算时,不要按照惯有思维将数据扩大100倍,而是应该直接将其扩大128倍。
Ø 利用右移实现除法运算
FPGA设计中要极力避免除法,甚至是严禁使用“ /”来用于除法计算。这是由于除法器会占用极大的资源,其占用资源量要多于乘法器,而且很多时候不能在一个时钟周期内得出结果。而当不得不使用除法的时候,应尽量使除法转化为除以2的N次方形式,这样便可以利用右移运算来实现该除法运算,从而大大减少硬件资源。
当除数是2的N次方的常数时,就可以用移位运算来实现除法。例如:a/2,等价于 a>>1;a/4等价于a>>2;a/8等价于a>>3,依此类推。
与左移不同的是,当除数不是2的N次方的常数时,不能简单地通过移位运算来简化实现。
总而言之,在FPGA设计中应尽力避免除法。
Ø 利用左移位产生独热码
独热码,也叫one-hot code,就是只有1个比特为1,其他全为0的一种码制。例如8’b00010000,8’b1000000等。
独热码在设计时非常有用,可以用来表示状态机的状态使状态机更健壮,也可以用于多选一的电路中,表示选择其中的一个。
利用左移位操作,可以方便地产生独热码,例如产生4’b0010,可以是4’b1 << 1。类似地,也可以产生1个比特为0,其他为1的码制。例如产生4’b1011,可以是~(4’b1 <<2)。利用左移操作,还可以产生其他需要的数字结果:
例如,产生5’b00111,可以是(5’b1<<3)-1。
例如,产生5’b11100,可以是~((5’b1<<2)-1)。
5.8 条件运算符
|
分类 |
情况 |
功能 |
代码 |
电路示意图 |
备注 |
|
选择器
|
常见形式1 |
通过S,选择输入给输出C。 |
always@(*)begin case(S) 2’b00 : C=D0; 2’b01 : C=D1; 2’b10 : C=D2; default : C= D3; endcase end |
|
|
|
常见形式2 |
通过S,选择输入给输出C。 |
always@(*)begin C = D[S]; end |
|
此时代码亦常用,其本质也是选择器。 |
|
|
用if-else |
通过判断s来选择。 |
always@(*)begin if(S==0) C=D0; else if(S==2’b01) C=D1; else C=D2; end |
|
请注意此处用到了相等比较器和选择器。 |
5.8.1 三目运算符
Verilog HDL语法中条件运算符(?:)带有三个操作数(即三目运算符),其格式一般表达为:
SHAPE * MERGEFORMAT
|
条件表达式?真表达式:假表达式; condition_expr? true_expr : false_expr;
|
其含义为:当“条件表达式”为真(即逻辑1),执行“真表达式”;当“条件表达式”为假(即逻辑0),执行“假表达式”。即当condition_expr为真(即值为1),选择true_expr;如果condition_expr为假(值为0),选择false_expr。如果condition_expr为x 或z ,结果将是按以下逻辑true_expr和false_expr按位操作的值: 0与0得0,1与1得1,其余情况为x 。
应用举例如下:
|
1 2 3 |
always@(*)begin r =s ? t : u ; end |
在上面的表达式中s如果为真,则把t赋值给r;如果s为假,则把u赋值给r。
对应硬件电路图如下所示。

图1.3- SEQ 图1.3- * ARABIC27案例对应硬件电路
条件运算符的使用有以下几点需要注意的地方:
(1)条件表达式的作用实际上类似于多路选择器,如图1.3-8所示。同时,其可以用if-else语句来替代。
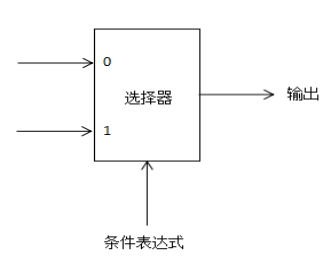
图1.3- SEQ 图1.3- * ARABIC282选1多路选择器图
(2)条件运算符可用在数据流建模中的条件赋值,这种情况下条件表达式的作用相当于控制开关。例如:
|
1 2 |
wire[2:0] student ; assign student = Marks >18 ?Grade_A:Grade_C ; |
其中,表达式Marks > 18如果为真,则Grade_A赋值为student;如果Marks > 18为假,则Grade_C赋值为student。
对应硬件电路图如下所示。
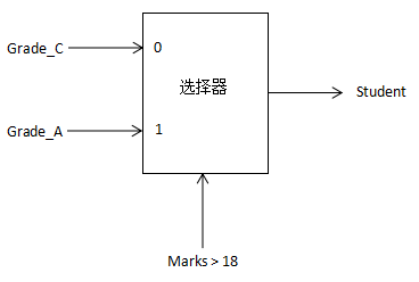
图1.3- SEQ 图1.3- * ARABIC29对应硬件电路图
(3)条件运算符也可以嵌套使用,每个“真表达式”和“假表达式”本身就可以是一个条件表达式。例如:
|
1 2 |
reg OUT,M,CTL,CLT,A,B,C,D; assign OUT = (M = = 1)?(CTL ? A:B):(CLT ? C:D); |
上面代码所代表的含义是:表达式M == 1如果为真,则判断CTL是否为真,如果CTL为真就将A赋值给OUT,如果为假就将B赋值给OUT;如果M = = 1为假,则判断CLT是否为真,如果CLT为真就将C赋值给OUT,如果为假就将D赋值给OUT。
对应硬件电路图如下所示。
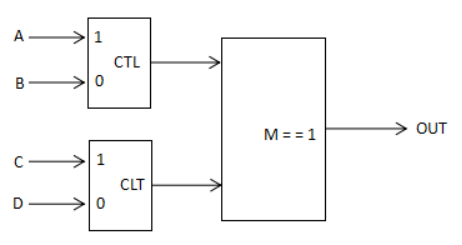
图1.3- SEQ 图1.3- * ARABIC30对应硬件电路图
5.8.2 if语句
“if”语句的语法如下:
if(condition_1)
procedural_statement_1;
{else if(condition_2)
procedural_statement_2};
{else
procedural_statement_3};
其含义为:如果对condition_1 条件满足,不管其余的条件是否满足,都执行procedural_statement_1,procedural_statement_2和procedural_statement_3都不执行。
如果condition_1不满足而condition_2满足,则执行procedural_statement_2,而procedural_statement_1和procedural_statement_3都不执行。
如果condition_1不满足并且condition_2也不满足时,执行procedural_statement_3,而procedural_statement_1和procedural_statement_2都不执行。
通过下面一个例子来具体说明:
if(Sum < 60) begin
Grade = C;
Total_C = Total _C + 1;
end
else if(Sum < 75) begin
Grade = B;
Total_B = Total_B + 1;
end
else begin
Grade = A;
Total_A = Total_A + 1;
end
注意条件表达式必须总是用括号括起来,如果使用if - if - else 格式,那么可能会有二义性,如下面的示例所示:
if(Clk)
if(Reset)
Q = 0;
else
Q = D;
这里存在一个疑问:最后一个else 属于哪一个if语句? 是属于第一个if 的条件(Clk)还是属于第二个if的条件 (Reset)? 这在Verilog HDL 中已通过将else 与最近的没有else 的if语句相关联来解决。在这个例子中, else 与内层if 语句相关联。
下面再举一个if 语句的例子:
if(Sum < 100)
Sum = Sum + 10;
if(Nickel_In)
Deposit = 5;
Elseif (Dime_In)
Deposit = 10;
else if(Quarter_In)
Deposit = 25;
else
Deposit = ERROR;
建议:
1、条件表达式需用括号括起来。
2、若为if - if 语句,请使用块语句 begin --- end,如下所示。
if(Clk) begin
if(Reset)
Q = 0;
else
Q = D;
end
以上两点建议是为了使代码更加清晰,防止出错。
5.8.3 case语句
case 语句是一个多路条件分支形式,其语法如下:
case(case_expr)
case_item_expr{case_item_expr} :procedural_statement
. . . . . .
[default:procedural_statement]
endcase
case语句下首先对条件表达式case_expr求值,然后依次对各分支项求值并进行比较,执行第一个与条件表达式值相匹配的分支中的语句。可以在1个分支中定义多个分支项,且这些值不需要互斥。缺省分支覆盖所有没有被分支表达式覆盖的其他分支。
例:
case (HEX)
4'b0001 : LED = 7'b1111001; // 1
4'b0010 : LED = 7'b0100100; // 2
4'b0011 : LED = 7'b0110000; // 3
4'b0100 : LED = 7'b0011001; // 4
4'b0101 : LED = 7'b0010010; // 5
4'b0110 : LED = 7'b0000010; // 6
4'b0111 : LED = 7'b1111000; // 7
4'b1000 : LED = 7'b0000000; // 8
4'b1001 : LED = 7'b0010000; // 9
4'b1010 : LED = 7'b0001000; // A
4'b1011 : LED = 7'b0000011; // B
4'b1100 : LED = 7'b1000110; // C
4'b1101 : LED = 7'b0100001; // D
4'b1110 : LED = 7'b0000110; // E
4'b1111 : LED = 7'b0001110; ,// F
default:LED = 7'b1000000; // 0
endcase
书写建议: case语句的缺省项必须写,防止产生锁存器。
5.8.4 选择语句
Verilog语法中有一个常用的选择语句,其语法形式为:
vect[a +: b]或vect [a -: b];
vect为变量名字,a为起始位置,加号或者减号代表着升序或者降序,b表示进行升序或者降序的宽度。
vect[a +: b]等同于vect[a : a+b-1],vect的区间从a开始向大于a的方向进行b次计数;vect [a -: b]等同于vect[a : a-b+1],vect的区间从a开始向a小的方向进行b次计数。a可以是一个常数也可以是一个可变的数,但b必须是一个常数。
例1:vect[7 +: 3];
其中,起始位置为7,+代表着升序,宽度为3。即从7开始向比7大的方向数3个数。其等价形式为:vect[7 +: 3]==vect[7 : 9]。
例2:vect[9 -: 4];
其中,起始位置为9,-代表着降序,宽度为4。即从9开始向比9小的方向数4个数。其等价形式为:vect[9 -: 4]==vect[9 : 6]。
在实际使用的过程中该语法最常用的形式是将a作为一个可变的数来使用。例如需要设计具有如下功能的代码:
当cnt==0时,将din[7:0]赋值给data[15:8];当cnt==1时将din[7:0]赋值给data[7:0]。
在设计的时候便可以写成:data[15-8*cnt -: 8] <= din[7:0](此时需要将15-8*cnt视为一个整体a,其会随着cnt变化而发生变化),这样一来就完成了对代码的精简工作。
选择语句的硬件电路结构如下图所示,其本质上是一个选择器。当cnt==0时,选中data[15:8]的锁存器,将din[7:0]赋值给data[15:8],而data[7:0]的锁存器保持输出不变;当cnt==1时,选中data[7:0]的锁存器,将din[7:0]赋值给data[7:0],而data[15:8]的锁存器保持输出不变。
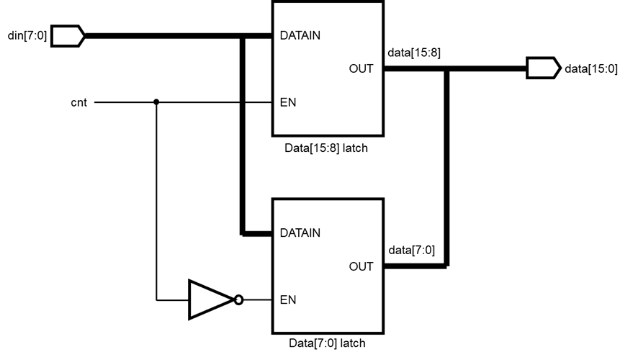
图1.3- SEQ 图1.3- * ARABIC31选择语句硬件电路图
用Modelsim对以上例子进行功能仿真后的仿真图如下所示。
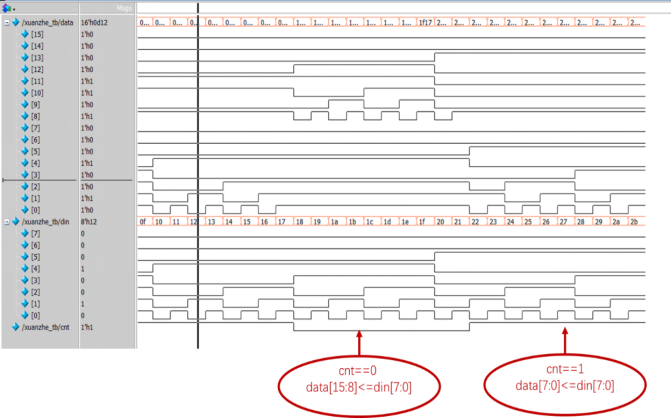
图1.3- SEQ 图1.3- * ARABIC32仿真的波形图
可以看出仿真结果满足实际的设计需求。
经验总结:在实际工程中可以多使用选择语句vect[a +: b]或vect [a -: b]的形式来进行代码编写,这将有助于精简设计代码。
5.8.5 经验总结
if 语句和case语句是Verilog里两个非常重要的语句, if 和 case语句有一定的相关性,也有一定的区别。相同的地方在于两者几乎可以实现一样的功能,下面主要介绍一下两者之间的区别。
if 语句每个分支之间是有优先级的,综合得到的电路是类似级联的结构。case语句每个分支是平等的,综合得到的电路则是一个多路选择器。因此,多个if else-if语句综合得到的逻辑电路延时有可能会比case语句稍大。对于初学者而言,在一开始学习Veriolg的过程中往往喜欢用if else-if语句,因为这种语法表达起来更加直接。但是在运行速度比较关键的项目中,使用case语句的效果会更好。下面通过一个具体的案例来对比一下,使用if语句和case语句来描述同一功能电路的综合结果。
首先是用if语句写的代码:
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
module if_case( input [1:0] en, input [1:0] a, output reg q ); always @(*)begin if(en[0]==1) q = a[0]; else if(en[1]==1) q = a[1]; else q = 0; end endmodule |
其综合后的RTL视图如下所示。

图1.3- SEQ 图1.3- * ARABIC33if语句综合后的RTL视图
从上图中所示的RTL图可以看到,此电路中含有两个二选一多路选择器,并且右边的优先级要高于左边(因为q的值是直接与右边的二选一选择器连接),当en[0]不为1时才会继续判断en[1]。也就是说,在if语句下综合出的电路含有优先级。
接下来分析一下使用case语句描述的代码。
|
1 2 3 4 5 6 7 8 |
always @(*)begin case(en) 2'b01: q = a[0]; 2'b10: q = a[1]; default:q = 0; endcase end |
其综合后的RTL视图如下所示:
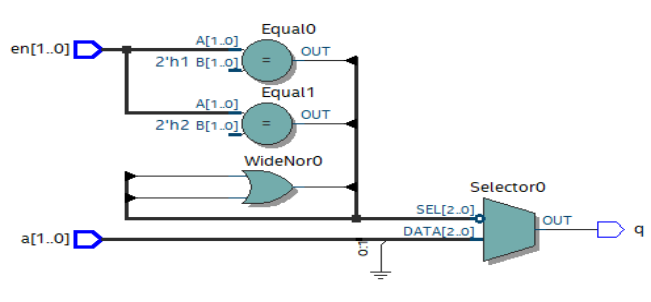
图1.3- SEQ 图1.3- * ARABIC34case语句综合后的RTL视图
可以看出,使用case语句编写的逻辑代码综合出的电路是并行的,没有优先级,不影响电路的运行速度。
虽然在RTL视图中,两种语句综合出的电路存在着较大的差别,但是由于目前的开发工具已经足够智能,在布局布线的时候会自动对电路进行优化,其最终映射到FPGA内部的电路之间基本毫无差别。
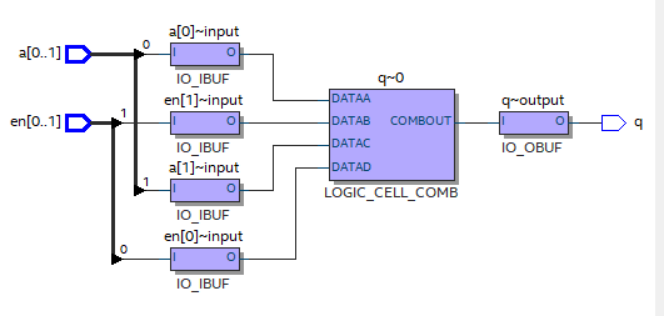
图1.3- SEQ 图1.3- * ARABIC35if语句映射后的电路
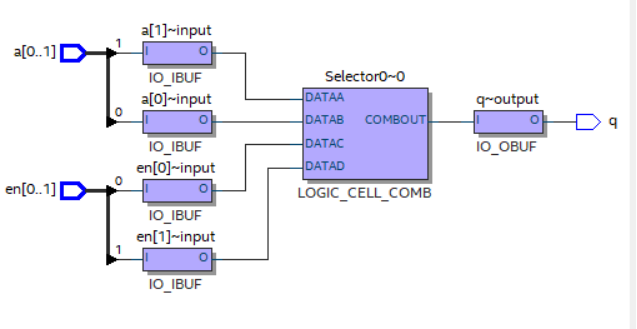
图1.3- SEQ 图1.3- * ARABIC36case语句映射后的电路
最后总结一下if语句和case语句之间的区别与联系:
If语句具有优先级,当if下的条件不满足时才执行else后面的部分。而case语句是并行的,没有优先级,这在两者综合出来的RTL视图中可以明显的观察出来。但由于现在的仿真和综合工具已经足够强大,最后综合后的结果if..else...与case...语句其实并无不同,只不过是两种不同的实现方式而已,因此基本上不用考虑这两者间的区别。在不影响功能的前提下设计师不需要做局部的优化工作,例如不需要考虑if/case语句的资源耗费差异、不需要考虑优化电路。只有在影响功能(即时序约束报错)的前提下,根据提示对电路进行优化。
5.9 拼接运算符
|
情况 |
功能 |
verilog代码 |
电路示意图 |
备注 |
|
拼接 (符号:{}) |
将大括号内的内,按位置一对一连接 |
reg[3:0] A; reg[2:0] B; always@(*)begin B={A[2],A[3],A[0]}; end |
|
拼接,实际上是选哪线相连。 |
拼接操作是将小表达式合并形成大表达式的操作,其形式如下:
{expr1, expr2, . . .,exprN} ;
拼接符是不消耗任何硬件资源的,其只是把线换一种组合方式,可以参照如下实例:
|
1 2 3 4 5 |
wire [7:0] Dbus;; assign Dbus [7:4] = {Dbus [0], Dbus [1], Dbus[2], Dbus[ 3 ] } ; / /以反转的顺序将低端4 位赋给高端4 位。 assign Dbus = {Dbus [3:0], Dbus [ 7 : 4 ] } ; / /高4 位与低4 位交换。 |
由于非定长常数的长度未知, 不允许连接非定长常数。因此如下所示代码是不符合语法规定的。
{Dbus,5} ;/ /不允许连接操作非定长常数。
第6节 功能描述-时序逻辑
6.1 always语句
时序逻辑的代码一般有两种:同步复位的时序逻辑和异步复位的时序逻辑。在同步复位的时序逻辑中复位不是立即有效,而在时钟上升沿时复位才有效。其代码结构如下:
always@(posedge clk) begin
if(rst_n==1’b0)
代码语句;
else begin
代码语句;
end
end
在异步复位的时序逻辑中复位立即有效,与时钟无关。其代码结构如下:
always@(posedge clk or negedge rst_n) begin
if(rst_n==1’b0)
代码语句;
else begin
代码语句;
end
end
针对时序逻辑的verilog设计提出以下建议:
为了教学的方便代码统一采用异步时钟逻辑,建议同学们都采用此结构,这样设计时只需考虑是用时序逻辑还是组合逻辑结构来进行代码编写即可。在实际工作中请遵从公司的相应规范进行代码设计。
使用GVim软件打开代码后,输入“Zuhe”命令后回车可得到组合逻辑的代码结构,输入“Shixu”命令后回车可得到时序逻辑的代码结构。
没有复位信号的时序逻辑代码设计是不规范的,建议不要这样使用。
6.2 D触发器
数字电路中介绍了多种触发器,如JK触发器、D触发器、RS触发器、T触发器等。在FPGA中使用的是最简单的触发器——D触发器。
6.2.1 D触发器结构
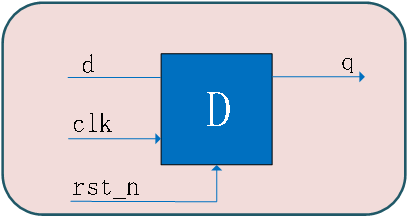
图1.3- SEQ 图1.3- * ARABIC37D触发器的结构图
REF _Ref527121853 h图1.3- 37是D触发器的结构图,可以将其视为一个芯片,该芯片拥有4个管脚,其中3个是输入管脚:时钟clk、复位rst_n、信号d;1个是输出管脚:q。
该芯片的功能如下:当给管脚rst_n给低电平(复位有效),即赋值为0时,输出管脚q处于低电平状态。如果管脚rst_n为高电平,则观察管脚clk的状态,当clk信号由0变1即处于上升沿的时候,将此时d的值赋给q。若d是低电平,则q也是低电平;若d是高电平,则q也是高电平。
6.2.2 D触发器波形
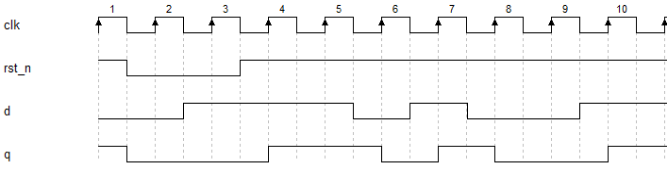
图1.3- SEQ 图1.3- * ARABIC38D触发器波形图
REF _Ref527121917 h图1.3- 38为D触发器的功能波形图,该波形图反映了D触发器各个信号的变化情况,从左到右表示时间的走势。从图中可以看到时钟信号有规律地进行高低变化。
按照从左向右的顺序观察波形图可以发现:
Ø 开始状态下,rst_n等于1,d等于0,q等于1。
Ø 随后rst_n由1变0,此时输出信号q立即变成0。对应的功能是:当给管脚rst_n低电平,也就是赋值为0时,输出管脚q处于低电平状态。
Ø 在rst_n为0期间,即使在有时钟或信号d发生变化的情况下q仍然保持为低电平。
Ø 在rst_n由0变成1撤消复位后,q没有立刻发生变化。
Ø 在第4个时钟上升沿时,此时rst_n等于1,而d等于1,因此q变成了1。
Ø 第5个时钟上升沿,仍然是同样情况,rst_n=1,d=1,因此q=1。
Ø 在第6个时钟上升沿,rst_n=1,d=0,因此q=0。
Ø 第7~10个时钟沿也是按同样方式判断。对应的功能是:如果管脚rst_n为高电平,则观察管脚clk,在clk由0变1即上升沿的时候,将现在d的值赋给q。若d是低电平,q也是低电平;若d是高电平,q也是高电平。
6.2.3 D触发器代码
首先,观察如下这段时序逻辑的代码:
|
1 2 3 4 5 6 7 8 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin q <= 0; end else begin q <= d; end end |
从语法上分析该段代码的功能为:该段代码总是在“时钟clk上升沿或者复位rst_n下降沿”的时候执行一次。具体执行方式如下:
1. 如果复位rst_n=0,则q的值为0;
2. 如果复位rst_n=1,则将d的值赋给q(注意,前提条件是时钟上升沿的时候)。
上例的功能与本案例的功能是相同的:当给管脚rst_n给低电平,也就是赋值为0时,输出管脚q就处于低电平状态。如果管脚rst_n为高电平则观察管脚clk,在clk由0变1即上升沿的时候,将现在d的值赋给q,d是低电平,q也是低电平,d是高电平,q也是高电平。
因此可以看出这段代码的功能与D触发器的功能是一样的,即该代码其实就是在描述一个D触发器,也就是D触发器的代码。
前文中已经讲过在FPGA设计中可以用原理图的形式来设计,也可以用硬件描述语言来设计。当用原理图来设计时几个D触发器还可以忍受,但如果出现几千几万个D触发器则必定是头晕眼花,而用硬件描述语言Verilog则不存在这一问题。
6.2.4 怎么看FPGA波形
下面来讨论如下图所示的波形,先观察在第4个时钟上升沿的时刻,思考一下此时看到的信号q的值是多少?是0还是1?或者观察到的是q的上升沿?

图1.3- SEQ 图1.3- * ARABIC39理想波形图
首先明确一点:Verilog代码对应的是硬件,因此应该从硬件的角度来分析这个问题。再来理清一下代码的因果关系:先有时钟上升沿,此为因,然后再将d的值赋给q,这才是结果。这个因果是有先后关系的,对于硬件来说这个“先后”无论是多么地迅速,也一定会占用一定时间,所以q的变化会稍后于clk的上升沿。例如下图就是硬件的实际变化情况。

图1.3- SEQ 图1.3- * ARABIC40实际波形图
图1.3- 40中就很容易看出,第4个时钟上升沿时刻对应的q值为0,也就是变化前的值。上面的波形虽然更将近于实际,但这样画图使这一过程非常复杂,且非必要操作。因此建议只需掌握这种看波形规则,即时钟上升沿看信号,是看到变化之前的值。
所以第4个时钟上升沿时,看到q值为0;在第6个时钟上升沿时,看到q值为1;在第7个时钟上升沿时,看到q值为0;在第8个时钟上升沿时,看到q值为1;在第10个时钟上升沿时,看到q值为0。注意一下,复位信号是在系统开始时刻或者出现异常时才使用,一般上电后就不会再次进行复位,也可以认为复位是一种特殊情况。
下面考虑正常使用的情况:无论是从功能上还是波形上,都可以看到信号q只在时钟上升沿才变化,而绝对不会在中间发生变化。在一般的数字系统中大部分信号之间的传递都是在同一个时钟下进行的,即大部分都是同步电路。跨时钟的电路占比非常小,属于特殊的异步电路。在本教材中,如果没有提前说明所有的案例、练习都默认为同步电路。
下面具体分析每个时钟下q信号的情况:
在rst_n由1变0时,q立刻变成0。
在第2个时钟上升沿,看到rst_n为0。按代码功能,q仍然为0。
在第3个时钟上升沿,看到rst_n为0。按代码功能,q仍然为0。
在第4个时钟上升沿,看到rst_n为1,d值为1,q值为0。按代码功能,q变成1。
在第5个时钟上升沿,看到rst_n为1,d值为1,q值为1。按代码功能,q变成1。
在第6个时钟上升沿,看到rst_n为1,d值为0,q值为1。按代码功能,q变成0。
在第7个时钟上升沿,看到rst_n为1,d值为1,q值为0。按代码功能,q变成1。
在第8个时钟上升沿,看到rst_n为1,d值为0,q值为1。按代码功能,q变成0。
在第9个时钟上升沿,看到rst_n为1,d值为0,q值为0。按代码功能,q变成0。
在第10个时钟上升沿,看到rst_n为1,d值为1,q值为0。按代码功能,q变成1。
6.3 时钟
时钟信号是每隔固定时间上下变化的信号。本次上升沿和上一次上升沿之间占用的时间就是时钟周期,其倒数为时钟频率。高电平占整个时钟周期的时间,被称为占空比。
FPGA中时钟的占空比一般是50%,即高电平时间和低电平时间一样。其实占空比在FPGA内部没有太大的意义,因为FPGA使用的是时钟上升沿来触发,设计师们更加关心的是时钟频率。
如果时钟的上升沿每秒出现一次,说明时钟的时钟周期为1秒,时钟频率为1Hz。如果时钟的上升沿每1毫秒出现一次,说明时钟的时钟周期为1毫秒,时钟频率为1000Hz,或写成1kHz。
现在普通FPGA器件所支持的时钟频率范围一般不超过150M,高端器件一般不超过700M(注意,该值为经验值,实际时钟的频率与其具体器件和设计电路有关),所对应的时钟周期在纳秒级范围。因此在本教材中所有案例的时钟频率一般选定范围是几十至一百M左右。
下面列出本教材常用到的时钟频率以及所对应的时钟周期,方便进行换算。
表1.3- SEQ 表1.3- * ARABIC11常用时钟频率及其对应时钟周期
|
时钟频率 |
时钟周期 |
|
100KHz |
10_000ns |
|
1MHz |
1_000ns |
|
8MHz |
125ns |
|
50MHz |
20ns |
|
100MHz |
10ns |
|
125MHz |
8ns |
|
150MHz |
6.667ns |
|
200MHz |
5ns |
时钟是FPGA中最重要的信号,其他所有信号在时钟的上升沿统一变化,这就像军队里的令旗,所有军队在看到令旗到来的时刻执行已经设定好的命令。
时钟这块令旗影响着整体电路的稳定。首先,时钟要非常稳定地进行跳动。就如军队令旗,如果时快时慢就会让人无所适从,容易出错。而如果令旗非常稳定,每个人都知道令旗的指挥周期,就可以判断令旗到来前是否可以完成任务,如果无法完成则进行改正(修改代码),从而避免系统出错。
其次,一个高效的军队中令旗越少越好,如果不同部队对标不同的令旗,那么部队协作就容易出现问题,整个军队无法高效的完成工作,容易出现错误。同样的道理,FPGA系统的时钟必定是越少越好,最好只存在一个时钟。
以上就是要求不要把信号放在时序逻辑敏感列表的原因。
6.4 时序逻辑代码和硬件
先来分析一下下面这段代码:
|
1 2 3 4 5 6 7 8 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin q <= 0; end else begin q <= a + d; end end |
仍然从语法上分析该段代码的功能。该段代码总是在“时钟clk上升沿或者复位rst_n下降沿”的时候执行一次。具体执行方法如下:
1. 如果复位rst_n=0,则q的值为0;
2. 如果复位rst_n=1,则将(a+d)的结果赋给q(注意,前提条件是时钟上升沿的时候)。
假设用信号c表示a+d的结果,则第2点可改为:如果复位rst_n=1,则将c的值赋给q(注意,前提条件是时钟上升沿的时刻)。很明显这是一个D触发器,输入信号为d,输出为q,时钟为clk,复位为rst_n,其电路示意图如下图所示:

图1.3- SEQ 图1.3- * ARABIC41时序逻辑对应的电路图
可知c是a+d的结果,因此其自然是通过一个加法器实现,画出上面代码所对应的电路结构图,可以看出在D触发器的基础上增加了一个加法器。
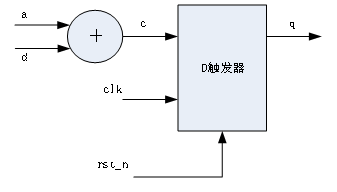
图1.3- SEQ 图1.3- * ARABIC42最终的电路图
很容易分析出上面电路的功能:信号a和信号b相加得到c,c连到D触发器的输入端。当clk出现上升沿时,将c的值传给q。这与代码功能是一致的。
下面是代码和硬件所对应的波形图。
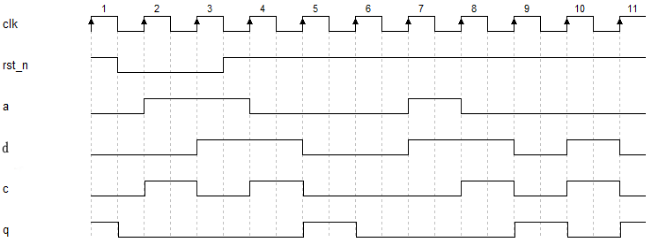
图1.3- SEQ 图1.3- * ARABIC43对应的波形图
先看信号c的波形:c的产生只有与a和d有关,与rst_n和clk无关。c是a+d的结果,按照二进制加法:0+0=0,0+1=1,1+1=0可以画出c的波形。
在第1个时钟期间,a=0,d=0,所以c=0+0=0;
在第2个时钟期间,a=1,d=0,所以c=1+0=1;
在第3个时钟期间,a=1,d=1,所以c=1+1=0;
在第4个时钟期间,a=0,d=1,所以c=0+1=1;
在第5到第6个时钟期间,a=0,d=0,所以c=0+0=0;
在第7个时钟期间,a=1,d=1,所以c=1+1=0;
在第8个时钟期间,a=0,d=1,所以c=0+1=1;
在第9个时钟期间,a=0,d=0,所以c=0+0=0;
在第10个时钟期间,a=0,d=1,所以c=0+1=1。
再看信号q的波形:q是D触发器的输出,其只在rst_n的下降沿或者clk的上升沿才变化,其他时刻不变化,即a、d、c发生变化时,q不会立刻发生改变。
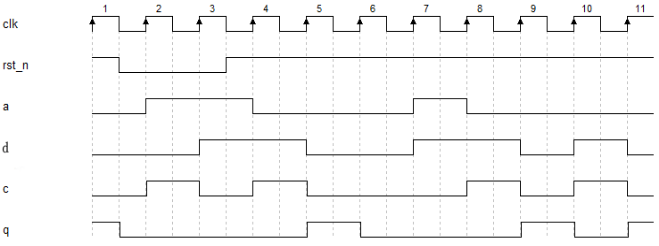
图1.3- SEQ 图1.3- * ARABIC44对应的波形图
下面具体分析每个时钟下q信号的情况:
在rst_n由1变0时,q立刻变成0。
在第2个时钟上升沿,看到rst_n为0。按代码功能,q仍然为0。
在第3个时钟上升沿,看到rst_n为0。按代码功能,q仍然为0。
在第4个时钟上升沿,看到rst_n为1,c值为0,q值为0。按代码功能,q变成0;
在第5个时钟上升沿,看到rst_n为1,c值为1,q值为0。按代码功能,q变成1;
在第6个时钟上升沿,看到rst_n为1,c值为0,q值为1。按代码功能,q变成0;
在第7个时钟上升沿,看到rst_n为1,c值为0,q值为0。按代码功能,q变成0;
在第8个时钟上升沿,看到rst_n为1,c值为0,q值为0。按代码功能,q变成0;
在第9个时钟上升沿,看到rst_n为1,c值为1,q值为0。按代码功能,q变成1;
在第10个时钟上升沿,看到rst_n为1,c值为0,q值为1。按代码功能,q变成0;
在第11个时钟上升沿,看到rst_n为1,c值为1,q值为0。按代码功能,q变成1。
在讨论时序逻辑的加法器时对加法器的输出c和D触发器的输出q分开进行讨论,就像两块独立的电路。同样的道理,在设计Verilog代码时也可以将其分开来进行编写。
先将下面的硬件电路用Verilog描述出来:

图1.3- SEQ 图1.3- * ARABIC45加法器硬件电路图
该电路对应的电路可以写成:
|
1 2 3 |
always @(*)begin c = a + d; end |
也可以写成:
|
1 |
assign c = a + d; |
上面的两段代码,都是描述同一加法器硬件电路。接着用Verilog对触发器进行描述。

图1.3- SEQ 图1.3- * ARABIC46D触发器硬件电路图
其代码的写法如下:
|
1 2 3 4 5 6 7 8 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin q <= 0; end else begin q <= c; end end |
最后可以看到,两段代码都有信号c,说明这两段代码是相连的,利用硬件连接起来可以变成如下图所示的电路。
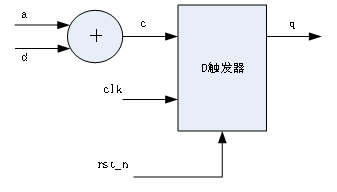
图1.3- SEQ 图1.3- * ARABIC47最终的硬件电路图
由此可见,下面两段代码所对应的硬件电路是一模一样的。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin q <= 0; end else begin q <= c; end end
always @(*)begin c = a + d; end |
|
1 2 3 4 5 6 7 8 |
always @(posedge clk or negedge rst_n)begin if(rst_n==1'b0)begin q <= 0; end else begin q <= a + d; end end |
那么这两种代码哪一种比较好呢?答案是这两段代码并无区别,因为两者的硬件是相同的。由此也可以得知评估verilog代码好坏的最基本标准,即不是看代码行数而是看硬件。
6.5 阻塞赋值和非阻塞赋值
在always语句块中,Verilog语言支持两种类型的赋值:阻塞赋值和非阻塞赋值。阻塞赋值使用“=”语句;非阻塞赋值使用“<=”语句。
阻塞赋值:在一个“begin…end”的多行赋值语句,先执行当前行的赋值语句,再执行下一行的赋值语句。
非阻塞赋值:在一个“begin…end”的多行赋值语句,在同一时间内同时赋值。
|
1 2 3 4 5 6 7 8 9 |
begin c = a; d = c + a; end
begin c <= a; d <= c + a; end |
上面两个例子中,1到4行部分是阻塞赋值,程序会先执行第2行,得到结果后再执行第3行。6至9行这一段是非阻塞赋值,第7行和第8行的赋值语句是同时执行的。
具体分析一下这两段代码这件的区别:假设当前c的值为0,d的值为0,a的新值为1。
阻塞赋值的执行过程和结果为:程序先执行第2行,此时c的值将更新为1,然后再执行3行,此时c+a也就是相当于1+1=2,即d的值为2。
非阻塞赋值的执行过程和结果为:程序同时执行第7行和8行。需要特别注意是,在执行第8行的时候,第7行还并未执行,这也就意味着c的值还没有发生变化,即此时c的值为0。同时执行的结果是,c的值为1,d的值为1。
根据规范要求,组合逻辑中应使用阻塞赋值“=”,时序逻辑中应使用非阻塞赋值“<=”。可以将这个规则牢牢记住,按照这一规则进行设计绝对不会发生错误。制定这个规范的原因并不是考虑语法需要,而是为了正确的进行硬件描述。













